前言
因为上课讲的听不懂,向量又是一个大块的,所以我觉得非常有必要开一片文章来做笔记不要再在原来的文章上堆史山啦。因为老师讲的完全没听懂,只能自己重新自学一遍,所以会从 OIwiki 等地方抄一些内容。以及这是笔记,是给我自己看的((
(你知道吗 $\overrightarrow{AB}$ 的 $\LaTeX$ 公式是 \overrightarrow{AB},噫,骇死我哩!)
基本定义
向量:既有大小又有方向的量称为向量,记作 $\vec{a}$ 或 $\alpha$。
自由向量:只有大小和方向的量,而起点并不固定,可以是任意位置。
有向线段:带有方向的线段称为有向线段,记作 $\overrightarrow{AB}$。有向线段有三要素:起点,方向,长度,知道了三要素,终点就唯一确定。一般使用有向线段表示向量。
向量的模:即向量的长度,记作 $|\overrightarrow{AB}|$。
单位向量:模长为 $1$ 的向量。
基底:在同一平面内的两个不共线的向量称为 基底。
基本运算
向量的加减法
$\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$,即先从 $A$ 点走到 $B$ 点,再从 $B$ 点走到 $C$ 点,等价于从 $A$ 点直接走到 $C$ 点。根据平行四边形法则可证向量加法具有交换律,且显然具有结合律。
$\vec{a}-\vec{b}=\vec{a}+(-\vec{b})$。与加法相同。当然减法也有几何意义:$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$。
如果用点表示向量,则若 $\vec{a}=(x_1,y_1),\vec{b}=(x_2,y_2)$ 则:
- $(x_1,y_1)+(x_2,y_2)=(x_1+x_2,y_1+y_2)$
- $(x_1,y_1)-(x_2,y_2)=(x_1-x_2,y_1-y_2)$
点与向量加法
$P+\vec{a}$ 表示将 $P$ 向 $\vec{a}$ 的方向平移 $|\vec{a}|$ 的距离(这么说可能不够准确,但是能理解就行),最终运算结果为一个点。
向量的数乘
实数 $p$ 与向量 $\vec{a}$ 相乘得到一个向量,记为 $p\vec{a}$,他有如下定义/性质:
- $|p\vec{a}|=|p||\vec{a}|$(注意分辨绝对值和模长的符号)
- 当 $p\gt 0$ 时,$p\vec{a}$ 与 $\vec{a}$ 同向;当 $p\lt 0$ 时,$p\vec{a}$ 与 $\vec{a}$ 方向相反。
若用点表示向量则若 $\vec{a}=(x,y)$,则 $p(x,y)=(px,py)$。
基本性质/定理
共线(平行)
两个非零向量 $\vec{a}$ 与 $\vec{b}$ 共线(平行),当且仅当存在一个实数 $p$ 使得 $\vec{b}=p\vec{a}$。
证明:如果存在实数 $p$ 使得 $\vec{b}=p\vec{a}$ 则 $\vec{a}\parallel \vec{b}$;若 $\vec{a}\parallel \vec{b}$ 那么一定存在正实数 $p$ 使得:当 $\vec{a}$ 与 $\vec{b}$ 同向时,$\vec{b}=p\vec{a}$,反向时 $\vec{b}=-p\vec{a}$。
当然我们一般不用这个来判断共线,而是使用后面讲的点积和叉积。
平面向量基本定理
定理内容:对于两个不共线的向量 $\vec{e_1}$ 和 $\vec{e_2}$ 存在唯一实数对 $(x,y)$ 使得与 $\vec{e_1},\vec{e_2}$ 共面的任意向量 $\vec{a}$ 满足 $\vec{a}=x\vec{e_1}+y\vec{e_2}$。
首先我们先来证明这个前置定理:
两个向量共线当且仅当存在不全为 0 的两个实数 $k_1,k_2$ 使得 $k_1\vec{e_1}+k_2\vec{e_2}=\vec{0}$。
首先先证明存在:
将 $\vec{e_1},\vec{e_2},\vec{a}$ 移动至 $O$。设 $\vec{a}$ 的终点为 $A$,过 $A$ 作直线 $l_1\parallel \vec{e_2}$,交 $\vec{e_1}$ 所在直线于 $B$,过 $A$ 作直线 $l_2\parallel \vec{e_1}$,交 $\vec{e_2}$ 所在直线于 $C$。
由平行四边形法则可得:设 $\overrightarrow{OB}=x\vec{e_1},\overrightarrow{OC}=y\vec{e_2}$,则 $\vec{a}=\overrightarrow{OB}+\overrightarrow{OC}=x\vec{e_1}+y\vec{e_2}$。
你也许需要一张图:
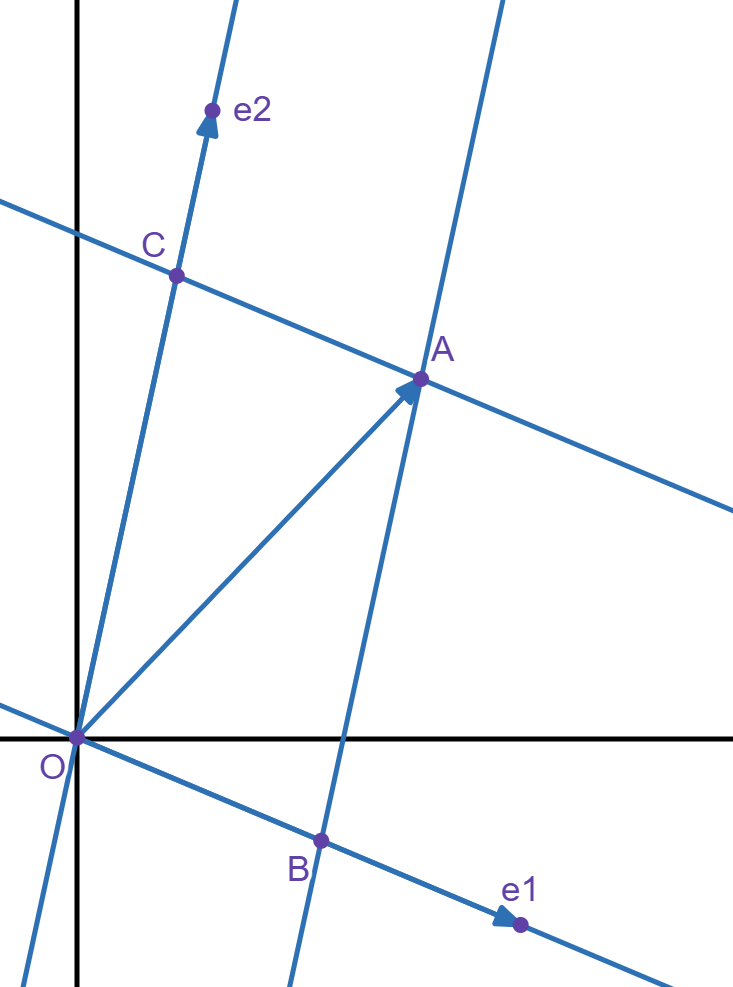
然后我们再来证明唯一性:
假设存在另一组解 $x’,y’$ 使得 $\vec{a}=x’\vec{e_1}+y’\vec{e_2}$,那么将两式相减得 $(x-x’)\vec{e_1}+(y-y’)\vec{e_2}=\vec{0}$,因为 $\vec{e_1},\vec{e_2}$ 不共线(线性无关),所以 $x-x’=0,y-y’=0$,解唯一。
向量的坐标表示
如果取与横轴正方向同向和与纵轴正方向同向的两个单位向量 $\vec{a},\vec{b}$ 作为一组基底,根据平面向量基本定理,平面上的所有向量与有序实数对 $(x,y)$ 一一对应。又因为有序实数对与坐标系中的点一一对应,因此坐标系中的点与向量一一对应。
一个更直观的理解是:对于任意一个有向线段 $\vec{OP}$ 显然与点 $P$ 一一对应,而只需要移动有向线段的起点就可以得到一个自由向量。因此自由向量与点一一对应。
对于一个有向线段 $\overrightarrow{AB}$,若 $A(x_1,y_1),B(x_2,y_2)$ 则 $\overrightarrow{AB}=(x_2-x_1,y_2-y_1)$。
点的平移
根据定义,若想平移 $P$,则可以将平移的方向和距离组合成一个向量,再与 $\overrightarrow{OP}$ 相加,得到的有向线段的终点即为结果。
点积与叉积
由于历史原因,数学学科和物理学科关于「inner product」和「outer product」两个词汇有着五花八门的翻译。
在物理学科,一般翻译成「标积」和「矢积」,表示运算的结果为标量和矢量。高中数学课本上「数量积」和「向量积」也采用了这种意译的办法。
在数学学科,通常也可以翻译成「内积」和「外积」,是两个名词的直译。「点乘」和「叉乘」是根据运算符号得来的俗称,这种俗称也很常见。
——OIwiki《内积和外积》
点积
定义
代数定义:对于两个向量 $\vec{a}=(x_1,y_1),\vec{b}=(x_2,y_2)$,$\vec{a}\cdot\vec{b}=x_1x_2+y_1y_2$。
几何定义:对于两个向量 $\vec{a},\vec{b}$ 和它们的夹角 $\theta$,$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos{\theta }$。
几何意义
首先我们定义投影向量:对于两个向量 $\vec{a},\vec{b}$,先将他们的起点都移动到点 $O$,从 $\vec{b}$ 的终点 $B$ 向 $\vec{a}$ 所在直线做一条垂线,垂足为 $P$,则 $\overrightarrow{OP}$ 就是 $\vec{b}$ 在 $\vec{a}$ 方向上的投影向量,$|\overrightarrow{OP}|$ 就是投影长度。
那么 $\vec{a}\cdot\vec{b}$ 就是 $\vec{a}$ 在 $\vec{b}$ 方向上的投影长度 乘以 $|\vec{b}|$。
两个向量的点积也可以反应出两个向量的方向关系,设 $\vec{a}$ 与 $\vec{b}$ 的夹角为 $\theta$,则:
- $\vec{a}\cdot\vec{b}\gt 0 \Leftrightarrow \cos{\theta} \gt 0$,即夹角为锐角。
- $\vec{a}\cdot\vec{b}=0 \Leftrightarrow \cos{\theta}=0$,即两向量垂直。
- $\vec{a}\cdot\vec{b}\lt 0 \Leftrightarrow \cos{\theta} \lt 0$,即夹角为钝角。
点积具有交换律和结合律,以及 ds 说的“乘数结合律”$(k\vec{a})\cdot\vec{b}=k(\vec{a}\cdot\vec{b})=\vec{a}\cdot(k\vec{b})$,其中 $k$ 为任意实数。
证明
首先我们需要前置知识余弦定理,即在 $\triangle ABC$ 中 $c^2=a^2+b^2-2ab \cos C$。
依旧是将向量的起点都移动到原点 $O$,即 $\vec{a}=\overrightarrow{OA},\vec{b}=\overrightarrow{OB},\overrightarrow{BA}=\vec{a}-\vec{b}$,那么在 $\triangle OAB$ 中:$|\overrightarrow{BA}|^2=|\vec{a}|^2+|\vec{b}|^2-2|\vec{a}||\vec{b}|\cos \theta$,进行如下公式推导:
$$\begin{array}{c} |\vec{a}-\vec{b}|^2=(\vec{a}-\vec{b})\cdot(\vec{a}-\vec{b})=\vec{a}\cdot\vec{a}-2\vec{a}\cdot\vec{b}+\vec{b}\cdot\vec{b} \\ |\vec{a}|^2+|\vec{b}|^2-2\vec{a}\cdot\vec{b}=|\vec{a}|^2+|\vec{b}|^2-2|\vec{a}||\vec{b}|\cos\theta\\ -2\vec{a}\cdot\vec{b}=-2|\vec{a}||\vec{b}|\cos \theta \\ \vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos \theta \end{array}$$
即可得到如下推论:
- $\vec{a}\perp \vec{b} \Leftrightarrow \vec{a}\cdot\vec{b}=0$
- $\operatorname{proj}_{\vec{b}}\vec{a}=\frac{\vec{a}\cdot\vec{b}}{|\vec{b}|}$(其中 $\operatorname{proj}$ 表示投影)
叉积
定义
代数定义:对于两个向量 $\vec{a}=(x_1,y_1),\vec{b}=(x_2,y_2)$,$\vec{a}\times\vec{b}=x_1y_2-y_1x_2$。
几何定义:对于两个向量 $\vec{a},\vec{b}$ 和它们的夹角 $\theta$,$|\vec{a}\times\vec{b}|=|\vec{a}||\vec{b}|\sin{\theta }$(注意分辨绝对值和模长符号)
几何意义
叉积的绝对值 $|\vec{a}\times\vec{b}|$ 等于以 $\vec{a}$ 和 $\vec{b}$ 为邻边构成的平行四边形的面积。这通常被用于计算两个共顶点的向量“围”成的三角形的面积,可惜我不会证明。
同点积一样,我们可以用叉积来判断两个向量的关系:
- 若 $\vec{a}\times\vec{b}\gt 0$ 则 $\vec{b}$ 在 $\vec{a}$ 的逆时针方向。
- 若 $\vec{a}\times\vec{b}\lt 0$ 则 $\vec{b}$ 在 $\vec{a}$ 的顺时针方向。
- 若 $\vec{a}\times\vec{b}=0$ 则 $\vec{b}\parallel \vec{a}$。
叉积具有反交换律(我不道啊 ds 说的) $\vec{a}\times\vec{b}=-(\vec{b}\times\vec{a})$ 和分配律($\vec{a}\times(\vec{b}+\vec{c})=\vec{a}\times\vec{b}+\vec{a}\times\vec{c}$),以及数乘结合律(上文讲过)。
证明
首先依旧有前置知识向量模公式 $|\vec{a}|=\sqrt{a_x^2+a_y^2}$ 和三角恒等式 $\sin^2\theta=1-\cos^2\theta$。
然后 ds 写了一大坨我看不懂了。
应用
这里的应用指的是在 OI 中的应用。
点与直线的位置关系
判断点 $P$ 在直线 $AB$ 的哪一侧:
- 若 $\overrightarrow{AB}\times\overrightarrow{AP}\gt 0$ 则 $P$ 在 $AB$ 的左侧(逆时针方向)。
- 若 $\overrightarrow{AB}\times\overrightarrow{AP}\lt 0$ 则 $P$ 在 $AB$ 的右侧(顺时针方向)。
- 若 $\overrightarrow{AB}\times\overrightarrow{AP}=0$ 则 $P$ 在 $AB$ 上。
线段相交
利用叉积判断每条线段的两个端点是否在另一条线段的两侧,若有两条线段 $AB,CD$,则若两线段相交,则 $(\overrightarrow{AB}\times\overrightarrow{AC})(\overrightarrow{AB}\times\overrightarrow{AD})\lt 0$ 且 $(\overrightarrow{CD}\times\overrightarrow{CA})(\overrightarrow{CD}\times\overrightarrow{CB})\le 0$。反过来也可以。
多边形面积
设一个任意的 $n$ 边形它的 $n$ 个顶点按逆时针顺序排序为 $P_0,P_1,\dots,P_n$,则它的面积 $S=\frac{1}{2}|\sum\limits_{i=0}^{n-1}P_i\times P_{i+1}|$。是的我依旧不会证明。
Code
没错是我们的模板库!
这计算几何我学了 6 个小时的理论,终于可以开始做题了。
namespace geo{
using db=double;
const db eps=1e-9;
bool is_zero(db x){return -eps<=x&&x<=eps;}
bool is_equal(db x,db y){
return y-eps<=x&&x<=y+eps;
}
struct Vec{
db x,y;
Vec(){}
Vec(int x,int y):x(x),y(y){}
Vec(db x,db y):x(x),y(y){}
friend Vec operator+(Vec a,Vec b){return Vec{a.x+b.x,a.y+b.y};}
friend Vec operator-(Vec a,Vec b){return Vec{a.x-b.x,a.y-b.y};}
Vec operator-(){return Vec{-x,-y};}
Vec operator*(db k){return Vec{x*k,y*k};}
Vec operator/(db k){return Vec{x/k,y/k};}
friend db operator^(Vec a,Vec b){return a.x*b.x+a.y*b.y;}//dot
friend db operator*(Vec a,Vec b){return a.x*b.y-a.y*b.x;}//det,但是注意不满足交换律
bool is_zero(){return geo::is_zero(x)&&geo::is_zero(y);}
db lenth(){return sqrt(x*x+y*y);}
friend ostream& operator<<(ostream& os,const Vec& v){
os<<v.x<<" "<<v.y;
return os;
}
friend istream& operator>>(istream& is,Vec& v){
is>>v.x>>v.y;
return is;
}
};
Vec projec(Vec a,Vec b){//投影向量
assert(!a.is_zero());
Vec v=a*((a^b)/(a^a));
return v;
}
}