前言
笔记笔记笔记。彩色有助于我们观察式子。
单调队列优化 DP
首先我们需要了解单调队列优化 DP,这里给出两个经典题目:P10978 Fence & P10977 Cut the Sequence。了解完后可以总结出一些规律:单调队列可以用于优化形如下式的 dp 转移方程式:
其中 $L(i),R(i)$ 是关于 $i$ 的单增/单减函数,$val(i,j)$ 能被拆成两部分,一部分只与 $i$ 有关,另一部分只与 $j$ 有关。
斜率优化
我们需要一道模板题:P5785 [SDOI2012] 任务安排。
弱化弱化版
弱化弱化版:P2365 任务安排,这里我们与原题统一一下,将 $f$ 数组改为 $c$。让我们先用这道题推出普通 DP 的状态转移方程。这里不讲怎么具体推导了,不会普通 DP 的先去学 DP 去。最后是可以得出这样的一个转移式子:
其中 $ts,cs$ 分别是 $t,c$ 的前缀和数组。
显然该算法复杂度为 $O(n^2)$,可以通过这题。
弱化版
弱化版:P10979 任务安排 2。这道题中 $n$ 从 5000 变成了 $3\times 10^5$,我们需要线性的做法。
考虑如何优化 DP,先将原转移方程的每一项展开:
其中 $\color{Red}ts_i\cdot cs_i$ 只与 $i$ 有关,$\color{Green} (ts_i+s)\cdot cs_j$ 与 $i$ 和 $j$ 都有关,$\color{Orange} s\cdot cs_n$ 是一个常数。
我们先只考虑 $\min\{\}$ 里的值,设括号里的这一坨式子等于 $a_j$,那么显然 $dp_i$ 就是 $a_j$ 的最小值。问题转换为:把 $i$ 当成一个定值,已知$ts,cs,s,dp_j$,我们需要求 $\min_{0\le j\lt i}a_j$:
做一下恒等变形得到:
这个式子长得就很像一次函数 $y=kx+b$:
将 $dp_j$ 和 $cs_j$ 看成坐标系中的一个点 $(cs_j,dp_j)$,定义一次函数 $y_j=kx_j-(ts_i\cdot cs_i-s\cdot cs_n+a_j)$ ,其中 $k$ 为定值 $(ts_i+s)$,则这是一条斜率为 $k$ 且过点 $(cs_j,dp_j)$ 的直线。
让我们将所有的 $(cs_j,dp_j)$ 和对应的一次函数都画在坐标系中,因为这些一次函数的斜率都相等,所以在最下面的函数对应的增量 $b$ 就是最小的,其对应的 $a_j$ 也就是我们要找的最小值。
如图,显然 $P2$ 对应的 $a_j$ 是我们要的最小值。
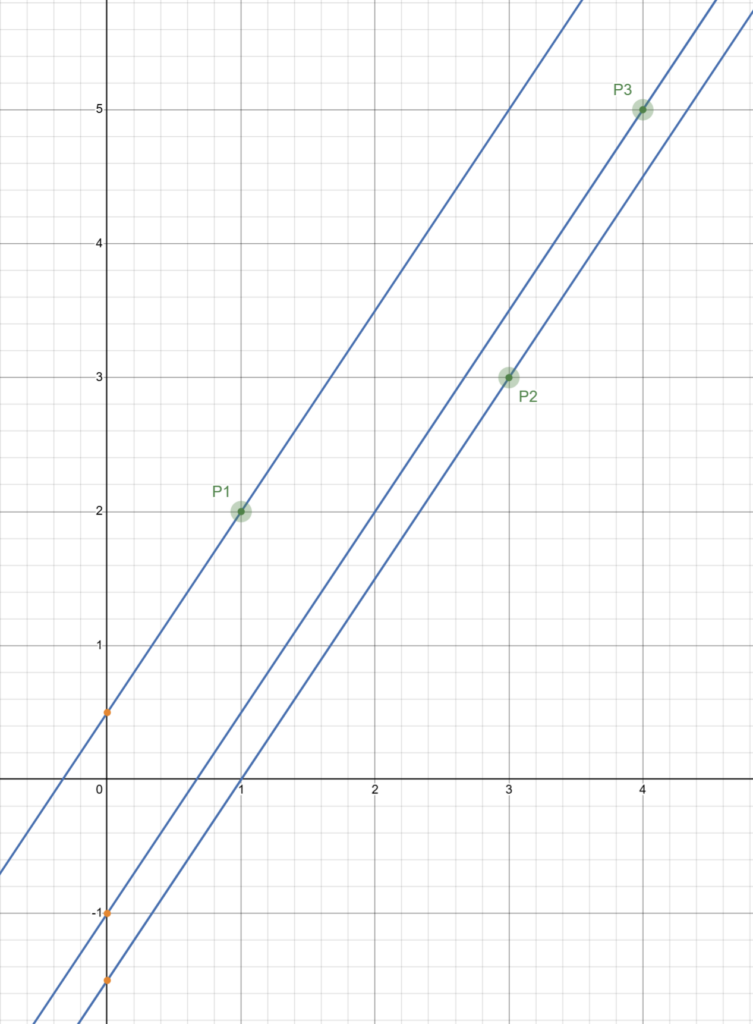
有了以上性质,让我们考虑如何维护答案。
由于每个 $i$ 对应的斜率 $k=ts_i+s$ 是单调递增的,因此如果存在位置关系如下图所示的三个点 $P1,P2,P3$ 时,$P2$ 一定不可能对任何一个 $dp_i$ 有贡献:
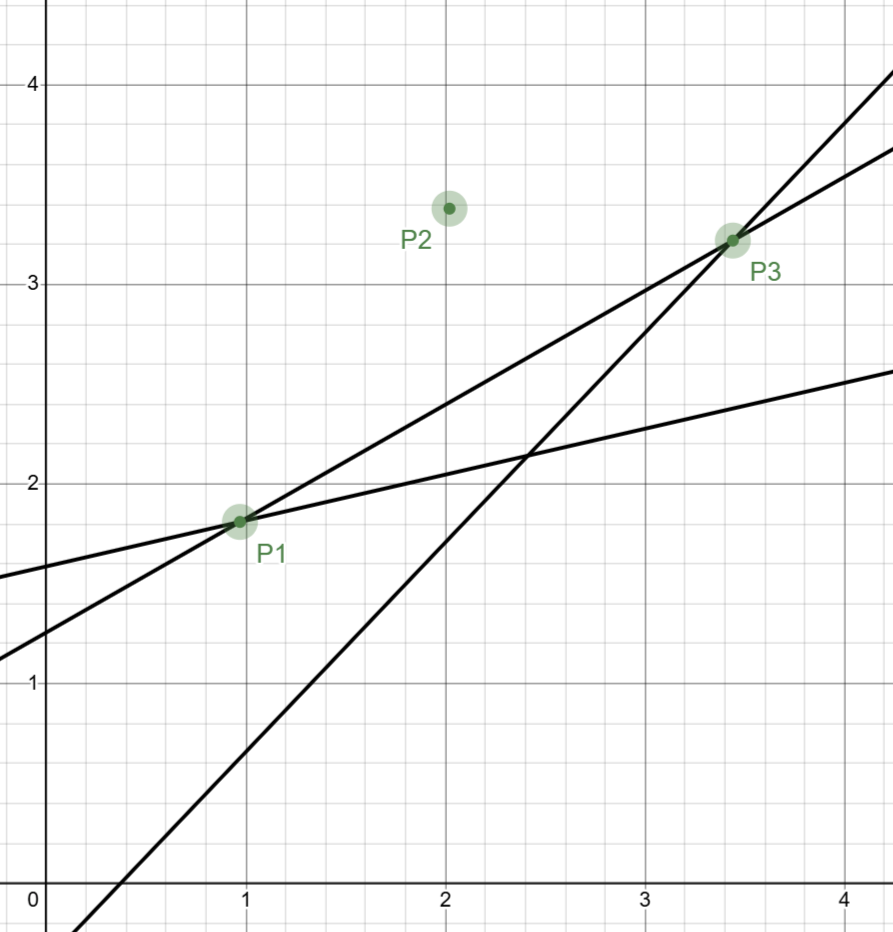
上图位置关系即 直线 $P1P2$ 的斜率 大于 直线 $P1P3$ 的斜率。
因此可能产生贡献的点围成的图形总是一个下凸壳,且相邻两点连成的直线的斜率一定大于等于 $i$ 对应的斜率 $k$,即:
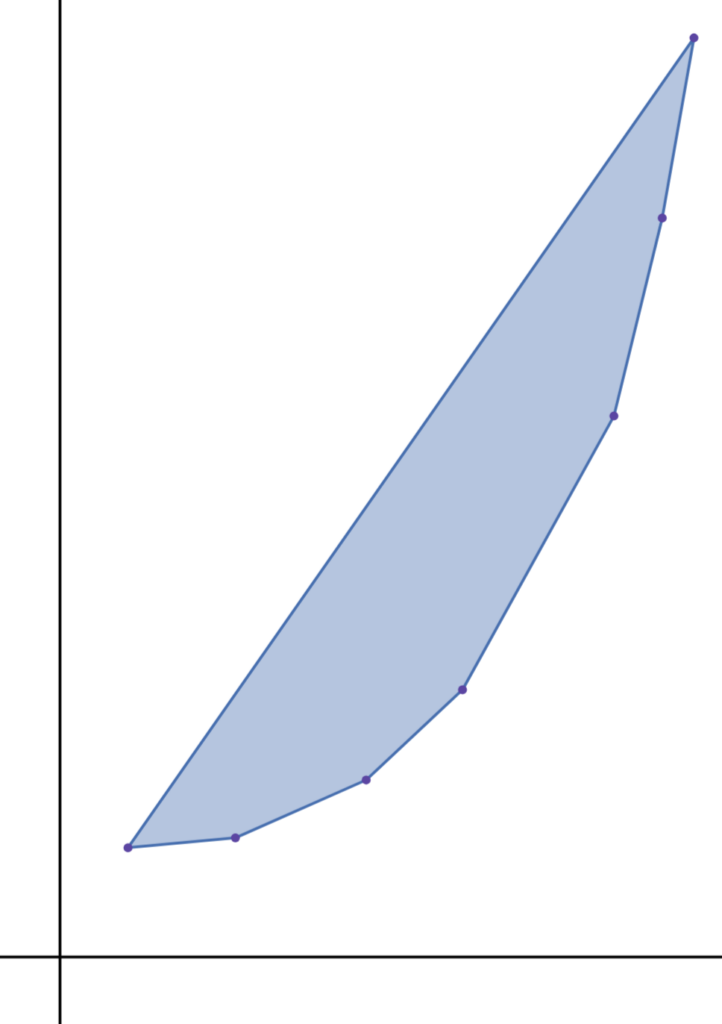
此时斜率为 $k$ 且过坐标系中最左边的点的直线,对应的 $a_j$ 就是 $dp_i$ 的最小值。
每当我们计算出一个新的点 $(cs_i,dp_i)$ 时就将它加入坐标系中,如果这个点与它的上一个点和上上个点满足 上上张图 中点的关系,就可以将它的上一个点从坐标系中删除。这样就保证了所有点组成一个下凸壳。
这个“坐标系”就是一个单调队列。
这里放出一份便于理解的代码,但由于题目卡浮点数计算斜率,这份代码并不能 AC(AC代码):
using ll=long long;
using db=long double;
int n,s;
cin>>n>>s;
vector<int>t(n+1),f(n+1);
vector<ll>ts(n+1),cs(n+1);
for(int i=1;i<=n;i++){
cin>>t[i]>>f[i];
ts[i]=ts[i-1]+t[i];
cs[i]=cs[i-1]+f[i];
}
vector<ll>dp(n+1,1e18);dp[0]=0;
deque<int>q;
q.eb(0);
auto slop=[&](int p1,int p2){
ll x1=cs[p1],x2=cs[p2],y1=dp[p1],y2=dp[p2];
return db(y1-y2)/(x1-x2);
};
for(int i=1;i<=n;i++){
if(q.empty())break;
ll k=ts[i]+s;
while(q.size()>=2&&slop(q[0],q[1])<k)q.pop_front();
int j=q.front();
dp[i]=dp[j]+ts[i]*(cs[i]-cs[j])+s*(cs[n]-cs[j]);
while(q.size()>=2&&slop(*----q.end(),q.back())>=slop(*----q.end(),i))q.pop_back();
q.emplace_back(i);
}
cout<<dp[n]<<endl;原版
还没学。