前言
学 OI 记的笔记。决定还是写给自己看,让我能在学过后如果忘了可以回来复习,不打算能让没学过的人听懂。
等待添加的内容:
对拍
这个是对拍,这个也是对拍。对拍通常由 4 个程序组成:要对拍的程序(zj.cpp),一定对的暴力程序(bl.cpp),造数据程序(sj.cpp),对拍程序(dp.cpp)。
造数据程序一般很好写(如果不怕挂分的话不好写就不写了),对拍程序就是模版,背下来就是了:
#include<bits/stdc++.h>
using namespace std;
int main(){
system("g++ -O2 zj.cpp -o zj -Wall -static -std=c++14");
system("g++ -O2 bl.cpp -o bl -Wall -static -std=c++14");
system("g++ -O2 sj.cpp -o sj -Wall -static -std=c++14");
int t=1e8;
for(int i=1;i<=t;i++){
FILE *fp=fopen("seed.in","w");
fprintf(fp,"%d",i);
fclose(fp);
system("./sj < seed.in > dp.in");
system("./bl < dp.in > dp.ans");
double st=clock();
system("./zj < dp.in > dp.out");
double ed=clock();
cout<<i<<" "<<ed-st<<" ms\n";
if(system("diff dp.out dp.ans")){
cout<<"WA\n";
break;
}
}
return 0;
}为了让数据随机,对拍程序每次会给造数据的程序输入一个 seed,造数据的程序只需要读入 seed 并设置随机种子即可。
写完后比赛全程让它在后台跑着就是了。
值得注意的是,rand 函数随机出的值在 windows 和 linux 下有所不同,windows 下 RAND_MAX=2^15,linux 下 RAND_MAX=2^31-1。以 linux 为例,如果我们想随机出一个小于等于 $2^{62}$ 的数,一种方法是将两个 rand 乘起来,但最后得到的结果并不会均匀的分布在 $[1,2^{62}]$ 之间(越在中间的出现越频繁,而且不难算出偶数出现的次数是奇数的三倍)。正确的做法是将 $2^{62}$ 拆成两个 $2^{31}$ 进行处理,即 ((ll)rand()<<31)|rand(),这样可以保证得到的数是相对均匀的分布在区间范围内的。
STL容器
这里只放一些关于语法的东西,对于具体的算法实现应该被放到数据结构等标题下。
常用成员函数功能
| 成员函数 | 功能 |
front/top | 访问容器中第一个/栈顶元素 |
back | 访问容器末尾元素 |
push/push_back/emplace/emplace_back | 向容器末尾添加元素 |
push/push_front/emplace/emplace_front | 向容器开头添加元素 |
pop/pop_back | 删除容器末尾元素 |
pop/pop_front | 删除容器开头元素 |
clear | 清空容器 |
insert/input | 在指定位置插入元素/范围 |
erase | 删除指定元素 |
size | 返回容器大小 |
empty | 检查容器是否为空 |
begin | 返回容器起始迭代器 |
end | 返回容器末尾迭代器+1(即--stl.end()才是末尾的迭代器) |
count | 查询匹配元素数量 |
lower_bound/upper_bound | 返回指向首个不小于/大于给定键的元素的迭代器(仅set,map等有序容器) |
迭代器
迭代器是可以遍历容器中元素的工具。它们提供了一种访问和操作元素的方式,而无需暴露容器的底层结构。迭代器可以被视为指向容器中元素的指针,但它们比指针更强大和灵活。
在 C++中,有多种类型的迭代器,每种都有不同的功能:
| 操作 | 输入迭代器 | 输出迭代器 | 前向迭代器 | 双向迭代器 | 随机访问迭代器 |
*it(读) | 1 | 1 | 1 | 1 | |
*it=(写) | 1 | 1 | 1 | 1 | |
++it/it++ | 1 | 1 | 1 | 1 | 1 |
--it/it-- | 1 | 1 | |||
it1==it2/it1!=it2 | 1 | 1 | 1 | 1 | |
| 默认构造 | 1 | 1 | 1 | ||
| 多趟遍历 | 1 | 1 | 1 | ||
it+x/it-x | 1 | ||||
it1-it2 | 1 | ||||
it[x] | 1 | ||||
it1<it2 | 1 |
其中“默认构造”指可以不提供任何参数就能创建迭代器对象的能力,“多趟遍历”指能够使用同一个迭代器范围进行多次遍历的能力(中译中:“可以创建多个迭代器指向同一个序列,这些迭代器可以独立移动且互不影响,可以反复从头开始遍历同一个序列”)
set,map 等容器提供双向迭代器,vector,deque 等容器提供随机访问迭代器,unordered_set,unordered_map 等容器提供向前迭代器。
对于迭代器 it 可以使用 prev(it)/next(it) 获得上一个/下一个迭代器(前提是支持--/++),这样我们就不用写繁琐的类似 a=*--it;++it;b=*++it;--it; 了。
标准输入/输出提供输入/输出迭代器,也就有一些豪玩的东西(?,例如可以这样输入输出数字:
vector<int>a;
istream_iterator<int>cin_it(cin),end;
while(cin_it!=end) {
a.emplace_back(*cin_it);
++cin_it;
}
ostream_iterator<int>out_it(cout," ");
for(auto v:a){
*out_it=v;++out_it;
}vector
当数组用的 vector。使用 emplace_back 优化 push_back,定义了赋值运算符。
使用 a.insert(a.end(),b.begin(),b.end()) 将 b 拼接在 a 的后面。
priority_queue
优先队列,通过二叉堆实现。默认为大根堆,可以通过传入参数重定义比较函数,以 tuple 举例:
using tp=tuple<int,int>;
priority_queue<tp,vector<tp>,greater<tp>>pq;//小根堆如果我们需要更复杂的比较函数可以这样写,以 int 举例(按 $a_i$ 从小到大排序):
vi a={1,1,4,5,1,4};
auto cmp=[&a](int x,int y){return a[x]>a[y];};//x>y
priority_queue<int,vector<int>,decltype(cmp)>pq(cmp);注意这里因为 priority_queue 是大根堆所以 cmp 相当于重定义了大于号,对于不同的 STL 容器,这里的参数的含义也是不一样的。
map 与 unordered_map
map 通过红黑树实现,单次操作复杂度 $O(\log)$;unordered_map 通过哈希实现,单次操作复杂度取决于哈希函数的冲突。因此两个容器不存在绝对的优劣,因为使用方法相近所以考场上写两个程序,通过大数据比较快慢。
map 可以用迭代器遍历,取地址后类型是一个 pair。
因为 map 由红黑树实现且可以通过迭代器从小到大遍历,所以显然维护的数据类型需要支持小于号运算符,我们可以用通过以下方法重定义运算符,以 {tuple,int} 举例:
using tp=tuple<int,int>;
//F1:
map<tp,int,greater<tp>>mp;
//F2:
auto cmp=[](tp x,tp y){
auto [x0,x1]=x;
auto [y0,y1]=y;
return x0!=y0?x0>y0:x1>y1;
};
map<tp,int,decltype(cmp)>mp(cmp);unordered_map 显然也需要数据类型有哈希函数,重定义的话以 struct S{unsigned int x,y;}; 举例(为尽量减少哈希冲突,将两个 uint 合成一个 ull):
struct S{
unsigned int x,y;
bool operator==(S a)const{
return x==a.x&&y==a.y;
}
};
struct SHash{
ull operator()(S a)const{
return (a.x<<32)+a.y;
}
};
unordered_map<S,int,SHash>ma;pair 有哈希函数,不用自己写。但是 tuple 就没有(
deque
双端对列,顾名思义就是两端都能执行 push,pop 和查询操作的队列。且支持随机访问。可以用两个数组手写实现。
需要注意的是 deque 的空间。不要开 1e6 个 deque(((
曾经这里写到可以用 list 代替 deque,但是用着用着我们就 TLE 了。使用程序测试 list 和 deque 的速度:
#include<bits/stdc++.h>
using namespace std;
int main(){
cin.tie(0)->sync_with_stdio(0);
int n,st,ed;
cin>>n;
deque<int>dq;
list<int>lst;
st=clock();
for(ll i=1;i<=n;i++){
dq.emplace_back(i);
dq.emplace_front(n-i);
}
ed=clock();
cout<<"deque:"<<ed-st<<"ms\n";
st=clock();
for(int i=1;i<=n;i++){
lst.emplace_back(i);
lst.emplace_front(n-i);
}
ed=clock();
cout<<"list:"<<ed-st<<"ms\n";
return 0;
}得到如下结果:
| $n=$ | deque 开O2/关O2(ms) | list 开O2/关O2(ms) |
| $10^5$ | 3/0 | 10/7 |
| $10^6$ | 15/4 | 97/59 |
| $5\times 10^6$ | 76/19 | 535/292 |
所以可以手写 deque 了,为了能够在考场上快速的写出来,就在定义时确定数组长度,不写动态开空间:
template<typename T>struct Deq{
vector<T>dq;
int head,tail;
Deq(int size=1e6):head(size),tail(size-1){
dq.resize(size*2+1);
}
void push_front(T x){dq[--head]=x;}
void push_back(T x){dq[++tail]=x;}
void pop_front(){head++;}
void pop_back(){tail--;}
T front(){return dq[head];}
T back(){return dq[tail];}
int size(){return tail-head+1;}
bool empty(){return head==tail+1;}
};set 与 multiset
集合与可重集,通过红黑树实现,单次复杂度 $O(\log)$ 但是常数巨大,大于线段树。
重定义比较运算,以 int 举例(跟 map 差不多):
set<int,decltype(cmp)>se(cmp);因为集合有序所以有成员函数 lower_bound 与 upper_bound,如需二分一定用成员函数,如果使用 lower_bound(se.begin(),se.end(),x) 则复杂度可达线性。
使用 insert 插入元素或范围,erase 删除元素或迭代器。在 multiset 中如果使用 erase 删除元素,那么容器中的所有相等元素都会被删除,应用 st.erase(st.find(x)) 来只删除一个 $x$。
数据结构
PS:

单调栈
顾名思义,单调栈即满足单调性的栈结构——OI-Wiki
单调栈的模板:P5788【模板】单调栈
核心就一句话:把栈顶比自己小的都扔了,然后把自己入栈,复杂度线性。代码不放了。
单调队列
顾名思义,单调队列的重点分为「单调」和「队列」。
「单调」指的是元素的「规律」——递增(或递减)。
「队列」指的是元素只能从队头和队尾进行操作。
——OI-Wiki
当然这里的队列指双端队列。
最常用的便是滑动窗口或者说区间最大值:P1886 滑动窗口 /【模板】单调队列
核心依旧一句话:比自己老还比自己小的扔掉,自己入队,太老的扔掉,复杂度线性。
原本这里放了代码,但是使用了 list,所以被删了。
并查集
并查集,顾名思义,是支持合并与查询操作的集合——沃兹基硕德
原理很简单:路径压缩。平均每次询问和查询的复杂度为常数,使用启发式合并(按秩合并)防止被卡,模板:P3367【模板】并查集
#include<bits/stdc++.h>
using namespace std;
int main(){
cin.tie(0)->sync_with_stdio(false);
int n,m;
cin>>n>>m;
vector<int>f(n+1);
iota(f.begin(),f.end(),0);
auto fa=[&](int x,auto&&fa){return f[x]=(f[x]==x?x:fa(f[x],fa));};
for(int i=1,op,x,y;i<=m;i++){
cin>>op>>x>>y;
int u=fa(x,fa),v=fa(y,fa);
if(op==1&&u!=v)f[v]=u;
if(op==2)cout<<(u==v)?'Y':'N')<<endl;
}
return 0;
}并查集还能再装一些“插件”:
扩展域: P1525[NOIP 2010 提高组] 关押罪犯,P2024[NOI2001] 食物链
伪删除:大概就是如果想把一个点从并查集删除,不需要真的移除,只要把它对集合的贡献减去即可。
树状数组
模板
一张图简介:
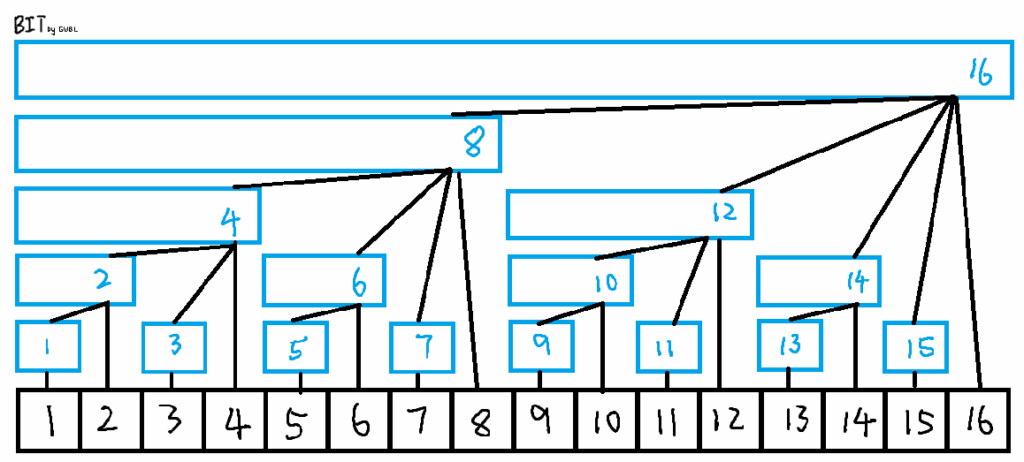
这是一颗有 $n$ 个节点数树,它满足以下性质:
- 对于节点 $x$,它所代表的区间长度(即上图蓝色区间)为 lowbit(x)。
- 对于节点 $x$,它的子节点个数为 lowbit(x) 在二进制下的位数。
- 除树根外,节点 $x$ 的父节点为 x+lowbit(x)。
- 树的深度为 $\log(n)$
读者自证不难
(设 $x$ 在二进制下最低位的 $1$ 为第 $y$ 位,则 lowbit(x)=$2^i$,即 $x\&-x$)
以单点修改前缀和查询举例,对于节点 $x$,我们记 $c_x$ 为该节点所对应的区间中的和,那么查询函数如下:
int cha(int x){
int ans=0;
while(x)ans+=c[x],x-=x&-x;
return ans;
}单点修改函数如下:
void add(int x,int d){
while(x<=n)c[x]+=d,x+=x&-x;
}它可以写的非常简洁!
当然这只是最基本的用法,树状数组可维护的东西只需满足答案可合并与可拆解,因此可以用它来维护区间修改单点查询,甚至区间修改区间查询。
这里放一段区间加区间和查询的代码(P3372【模板】线段树 1)
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
using vl=vector<ll>;
struct Bit{
int n;
vl c1,c2;//1区间带权和 2区间和
Bit(int n):n(n){
c1.resize(n+1);
c2.resize(n+1);
}
void add(int x,ll d){
int o=x;
while(x<=n){
c1[x]+=d*(x-o+1);
c2[x]+=d;
x+=x&-x;
}
}
ll cha(int x){
ll ans=0;
int o=x;
while(x){
ans+=(o-x)*c2[x]+c1[x];
x-=x&-x;
}
return ans;
}
};
int main(){
cin.tie(0)->sync_with_stdio(0);
int n,q;
cin>>n>>q;
vl a(n+1),qz(n+1);
for(int i=1;i<=n;i++){
cin>>a[i];
qz[i]=qz[i-1]+a[i];
}
Bit tr(n+1);
int op,x,y;
ll z;
while(q--){
cin>>op;
if(op==1){
cin>>x>>y>>z;
tr.add(x,z),tr.add(y+1,-z);
}else if(op==2){
cin>>x>>y;
cout<<tr.cha(y)-tr.cha(x-1)+qz[y]-qz[x-1]<<endl;
}
}
return 0;
}BIT上二分
例题:
现在有一个集合 $S=\{1,2,3,…,n\}$,给定 $n$ 次操作,第 $i$ 次给定一个数 $a_i$,你需要输出 $S$ 中第 $a_i$ 小的数并把它从集合中删除。
首先用树状数组维护一个桶,初始值 $1\sim n$ 都是 1,每次查询也就是找第一个前缀和等于 $a_i$ 的地方,删除即将这个位置从 $1$ 变为 $0$ 即可。
其中因为所有数都是非负整数,前缀和具有单调性,因此我们可以用二分查找,如果我们直接一个二分套一个树状数组,那么复杂度是 $O(\log^2)$ 的,但树状数组内部的一些数据是可以直接二分的,我们可以直接在树状数组查询的时候就二分:
首先我们记录一个指针 $x$ 表示当前二分到的区间,显然初始值应该为所有区间中“最上面”的一个区间,例如 $n=16$ 时 $x=16$,$n=15$ 时 $x=8$。接下来我们判断 $c_x$ 与 $k$ 的关系,如果 $c_x\ge k$,则说明最终要找的答案被包含在区间 $x$ 中,我们记录一个 $sc$ 表示“上一次满足关系的 $x$,方便最后输出;如果 $c_x\lt k$ 则说明答案不在区间 $x$ 中,我们就去找在 $x$ 后面的最大的一个区间,例如当 $x=8$ 时,我们下一步应该跳到 $x=12$。重复以上步骤直到区间 $x$ 的长度为 1。需要注意有的时候可能会使 $x\gt n$,显然我们需要让 $x$ 往下走,不能往后走。
int ef(int k){
int x=1<<(31-__builtin_clz(n)),sc=0;
while((x&-x)>1){
if(x>n||c[x]>=k)sc=x,x-=(x&-x)>>1;
else k-=c[x],x+=(x&-x)>>1;
}
return k-c[x]?sc:x;
}复杂度 $O(\log)$。
线段树
SegmentTreeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeee~~~
众所周知线段树在考场上是用来骗分的!
一张图简介:
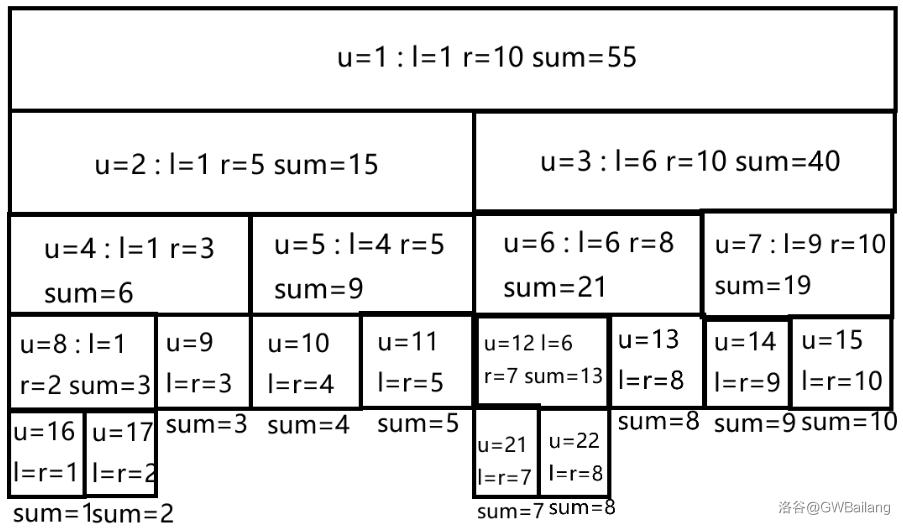
(你注意到图片能点了吗几百年前写的文章怎么这么【】)
线段树的功能取决于其 Merge 函数(懒修改函数随之而变),放个区间加区间和查询的模板:
struct Sgt{
struct sgt{
int l,r;
ll z;//<---
};
vector<sgt>tr;
vl tag;
vl a;
sgt Merge(sgt a,sgt b){//<---
return sgt{a.l,b.r,a.z+b.z};
}
void bud(int l,int r,int u){
if(l==r){tr[u]={l,r,a[l]};return;}
int mi=(l+r)/2;
bud(l,mi,u*2);
bud(mi+1,r,u*2+1);
tr[u]=Merge(tr[u*2],tr[u*2+1]);
}
Sgt(int n,vl a):a(a){
tr.resize(n*4+1);
tag.resize(n*4+1);
bud(1,n,1);
}
int jl(int u){return tr[u].r-tr[u].l+1;}
void lazy(int u){
tr[u*2].z+=jl(u*2)*tag[u];
tr[u*2+1].z+=jl(u*2+1)*tag[u];
tag[u*2]+=tag[u];
tag[u*2+1]+=tag[u];
tag[u]=0;
}
XDS cha(int l,int r,int u){
if(l<=tr[u].l&&tr[u].r<=r)return tr[u];
lazy(u);
int mi=(tr[u].l+tr[u].r)/2;
if(r<=mi)return cha(l,r,u*2);
else if(l>mi)return cha(l,r,u*2+1);
else return Merge(cha(l,r,u*2),cha(l,r,u*2+1));
}
void add(int l,int r,int u,int d){
if(l<=tr[u].l&&tr[u].r<=r){
tr[u].z+=d*jl(u);tag[u]+=d;
return;
}
lazy(u);
int mi=(tr[u].l+tr[u].r)/2;
if(r<=mi)add(l,r,u*2,d);
else if(l>mi)add(l,r,u*2+1,d);
else add(l,r,u*2,d),add(l,r,u*2+1,d);
tr[u]=Merge(tr[u*2],tr[u*2+1]);
}
};复杂度证明是个很有趣的东西,虽然我会,但是我懒得写了……
线段树的变种也有很多,可惜我不会。
图论
拓扑排序
一个我自己猜想的结论
拓扑排序时我们反向建边,然后最后得到的拓扑序反着输出,依旧能通过SPJ。至少这个结论在 这题 里是能AC的。以及这是我的证明,不知道是否严禁:
如何建反:将本应从 u 指向 v 的边连成从 v 指向 u 的边。
那么原本应该在v之前都走的点(只有这些点都走过才能走v),我反过来的做法会让这些点都在v之后走(也就是只有v走过才可能走这些点),最后得到的顺序整体翻过来,就是那些点都在v之前走完了。
字符串
公约
- 一般用 $n$ 表示字符串 $s$ 的长度
- 字符串默认下标从 0 开始
- 默认字符集为全部小写字母。对于回文串,可以通过在字符串中插入
#来只计算长度为奇数的回文串。 - 对于一个长度为 $n$ 的回文串 $s$,定义它的回文半径为 $\lceil\frac{n}{2}\rceil$。
最小表示法
对于一个字符串 $s$,我们可以从任意一个位置将其分割为两段,将前一段移动到后一段的后面遍可得到一个新的字符串 $t$,我们称 $s$ 和 $t$ 循环同构,能够得到的 $t$ 中字典序最小的字符串即为 $s$ 的最小表示法。
最暴力的做法就是枚举每个与 $s$ 同构的字符串并找到最小值。如何优化?对于与 $s$ 循环同构的 $a$ 和 $b$,设它们在 $s$ 中的起点分别为 $i,j$,设 $k$ 是最小使得 $a_k\neq b_k$ 成立的非负整数(通过暴力枚举得到)。我们不妨设 $a_k\le b_k$,那么以 $j\dots j+k$ 开头的所有字符串都不可能成为答案(如果以 $j+x(1\le x\le k)$ 开头,则一定不优于以 $i+x$ 开头),我们让 $j=j+k+1,k=0$ 然后继续枚举即可。便可得到以下代码:
s=s+s;//破环成链
int i=0,j=0,k=0;
while(i<n&&j<n&&k<n){
if(i==j)j++;
if(s[i+k]==s[j+k])k++;
else if(s[i+k]<s[j+k])j=j+k+1,k=0;
else i=i+k+1,k=0;
}
//ans=min(s.substr(i,n),s.substr(j,n));复杂度证明:因为每次循环时,$i,j$ 中都会有一个数至少加 1($k+1$ 等同于让 $i,j$ 的其中一个加 1),且 $0\le i,j\le n-1$,因此复杂度为 $O(n)$。
马拉车/Z算法
马拉车即 manacher,Z算法又称扩展 KMP,但是就像 CRT 和 EXCRT 一样 KMP 和 EXKMP 没有任何关系,不如叫扩展马拉车(((
manacher
求字符串 $s$ 的最长回文子串。
只考虑长度为奇数的回文串。我们用 $d_i$ 表示以 $s_i$ 为中心的最长回文串的回文半径,若我们已知 $d_0 \dots d_{i-1}$,设当前右端点最靠右的回文串的右端点为 $r$,中心为 $p$,则:
若 $i<r$,则 $d_i\ge \min(d_{p-(i-p)},r-i+1)$,证明如图(注意图中的 $r$ 标错了,应该是蓝色区间的右端点而不是区间的回文半径,且字母标少了,蓝色区间和橙色区间内的所有字母都应该能标出来):
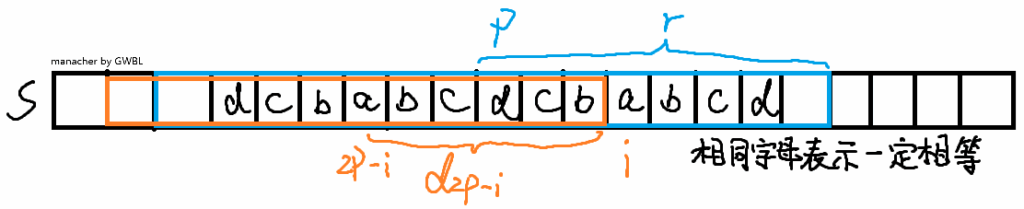
得到最小值后我们继续暴力求出 $d_i$。
便可得到以下代码:
//需要给s中间插入`#`
vi d(n,1);
int p=0,r=0;
for(int i=1;i<n;i++){
if(i<r)d[i]=min(d[p*2-i],r-i+1);
while(0<=i-d[i]&&i+d[i]<n&&s[i-d[i]]==s[i+d[i]])d[i]++;
if(i+d[i]-1>r)r=i+d[i]-1,p=i;
}
int ans=*max_element(d.begin(),d.end());
cout<<(ans*2-1)/2<<endl;Z算法
求 $z$ 数组,其中 $z_i$ 表示 $s[i\dots n-1]$ 与 $s$ 的最长公共前缀长度。
本质与马拉车一样,甚至代码复制过来改几个字符即可。
定义 $[i,i+z[i]-1]$ 为 $i$ 的 Z-box。若我们已知 $z_0\dots z_{i-1}$,且当前右端点最靠右的 Z-box 为 $[l,r]$,则:
若 $i<r$,则 $z_i\ge \min(z_{i-l},r-i+1)$,证明如图:
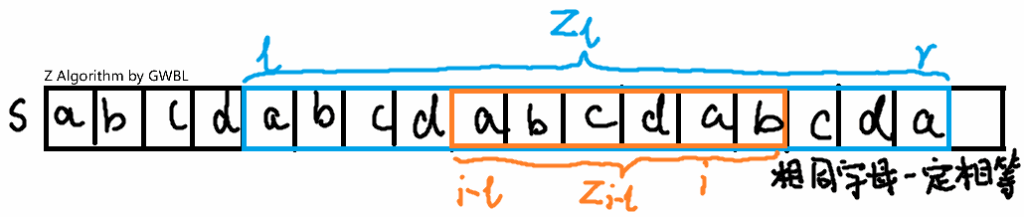
得到最小值后继续暴力求出 $z_i$。
便可得到以下代码:
vi z(n,0);
int l=0,r=0;
for(int i=1;i<n;i++){
if(i<r)z[i]=min(z[i-l],r-i+1);
while(i+z[i]<n&&s[z[i]]==s[i+z[i]])z[i]++;
if(i+z[i]-1>r)r=i+z[i]-1,l=i;
}
z[0]=n;复杂度证明
若执行 while 循环,则一定会更新 $r$,$r$ 单调递增,所以复杂度为 $O(n)$。——OI Wiki
但是我并不理解。
KMP
前缀数组
求数组 $\pi$,其中 $\pi_i$ 是使得 $s[i-k+1\dots i]=s[0\dots k-1]$ 且 $k\neq i$ 的最大的 $k$。
形式化的讲,就是求每个前缀中 真前缀和真后缀相等 的最长前缀(后缀)长度。
我们称一个字符串中,若有真前缀能与真后缀相等则称该真前缀为字符串的一个 Border。一个字符串可能有多个 Border,空串也算一个 Border。
依旧假设我们已知 $\pi_0\dots \pi_{i-1}$,来求 $\pi_i$。若 $t$ 是该前缀的一个 Border,则将 $t$ 的最后一个字符去掉后得到的 $t’$ 一定是 $s[0\dots i-1]$ 的一个 Border。所以如果 $s_{\pi_{i-1}}=s_i$,则该前缀的 Border 的最长长度一定为 $\pi_{i-1}+1$。
如果 $s_{\pi_{i-1}}\neq s_i$ 怎么办?我们考虑 $\pi_{\pi_{i-1}}$,令它等于 $j$ 则若 $s_j=s_i$,则 $\pi_i=j+1$,否则继续 $j=\pi_j$。这样循环下去直到求出 $\pi_i$ 或 $j=0$ 结束。若最终 $j=0$ 且 $s_j\neq s_i$ 则 $\pi_i=0$。
为方便,这里字符串下标从 1 开始。
vi pi(n+1);
for(int i=2;i<=n;i++){
int j=pi[i-1];
while(j>0&&s[j+1]!=s[i])j=pi[j];
j+=(s[j+1]==s[i]);
pi[i]=j;
}复杂度 $O(n)$,oi-wiki 上是这样说的:
关于 $O(n)$ 的时间复杂度,我们可以这样理解:首先根据代码,某一轮循环结束时的 $j$ 就是下一轮循环开始时的 $j$;根据前缀函数的定义,$\pi_{j – 1}\le j-1$,所以每次
j=pi[j]至少会使 $j$ 减少 1;又因为在 $i$ 的每轮循环中 $j$ 至多增加 1(第 5 行j++),因此 $n-1$ 轮循环中 $j$ 最多增加 $n-1$,又因为 $j$ 非负,因此整个算法中j=pi[j]的执行次数不会超过 $n-1$,所以时间复杂度为 $O(n)$.——Not Easy to Name(有 删 改)
子串查找
给定两个字符串 $s1$ 和 $s2$,求出 $s2$ 在 $s1$ 中所有出现的位置。
令 $s=s2+\#+s1$,我们求出 $s$ 的前缀数组 $\pi$,则从 $s1$ 在 $s$ 中对应的位置找,若 $\pi_i=|s2|$,则 $i$ 对应的在 $s1$ 中的位置即其前 $|s2|$ 个字符组成就是 $s2$。
说不清楚就把代码摆出来:
string s1,s2;
cin>>s1>>s2;
string s=" "+s2+"#"+s1;
int n=s.size()-1;
vi pi(n+1);
or(int i=2;i<=n;i++){
int j=pi[i-1];
while(j>0&&s[j+1]!=s[i])j=pi[j];
j+=(s[j+1]==s[i]);
pi[i]=(j==i?0:j);
}
for(int i=s2.size()+2;i<=n;i++){
if(pi[i]==s2.size())cout<<i-pi[i]-s2.size()<<endl;
}失配树
给定字符串 $s$ 和 $q$ 次询问,每次询问给出两个数 $x$ 和 $y$,求 $s[1\dots x]$ 与 $s[1\dots y]$ 的最长公共 Border。
我们在算出 $s$ 的前缀数组 $\pi$ 后,将节点 $i$ 与 $\pi_i$ 连接即可得到一颗树,且树根为 $0$。对于每次询问 $x,y$,求出它们的 LCA $f$,若 $f\neq x,f\neq y$ 则答案为 $s[1\dots f]$,否则 $f=\pi_f$,答案为 $s[1\dots f]$。
string s;
cin>>s;
s=" "+s;
int n=s.size()-1;
vi pi(n+1);
const int KMAX=20;
vector<vi>fa(KMAX+1,vi(n+1));
vector<vi>bian(n+1);
fa[0][1]=0,bian[0].eb(1);
for(int i=2;i<=n;i++){
int j=pi[i-1];
while(j>0&&s[j+1]!=s[i])j=pi[j];
j+=(s[j+1]==s[i]);
pi[i]=(j==i?0:j);
fa[0][i]=pi[i];
bian[pi[i]].eb(i);
}
vi dep(n+1);
function<void(int)>dfs=[&](int u){
for(auto v:bian[u]){
dep[v]=dep[u]+1;
int p=u;fa[0][v]=u;
for(int i=1;i<=KMAX;i++){
p=fa[i][v]=fa[i-1][p];
}
dfs(v);
}
};
dep[0]=1;
dfs(0);
auto lca=[&](int u,int v){
if(dep[u]>dep[v])swap(u,v);
for(int i=KMAX;i>=0;i--){
if(dep[fa[i][v]]>=dep[u]){
v=fa[i][v];
}
}
if(u==v)return u;
for(int i=KMAX;i>=0;i--){
if(fa[i][u]!=fa[i][v]){
u=fa[i][u];
v=fa[i][v];
}
}
return fa[0][u];
};
int q;
cin>>q;
while(q--){
int u,v;
cin>>u>>v;
int f=lca(u,v);
if(f==u||f==v)f=fa[0][f];
cout<<f<<endl;
}数学&数论
树学和树论与数学和数论。
gcd
俗称辗转相除法或辗转相减法,属于常识。C++ 有求 gcd 函数:__gcd。复杂度为 $O(\log(a+b))$。记得在求 gcd 之前判断会不会出现负数的情况(CSP-J2023 T3 令我印象深刻)。放下模板:
auto gcd=[&](int a,int b,auto&&gcd){return b?gcd(b,a%b,gcd):a;};区间加与 gcd
例题(P10463 Interval GCD):
给定一个长度为 $n$ 的序列 $a_i$,你需要做 区间加 和 区间查询 gcd 这两种操作。
乍一看加法跟 gcd 没关系,线段树没办法维护。
我们尝试从 gcd 的定义入手:$\gcd(a,b)=\gcd(b,a%b)$
取模跟加法还是没什么关系?别忘了 gcd 还有另一个名字,辗转相减法:$\gcd(a,b)=\gcd(a,b-a)$
这看起来跟加法有点关系了,因为 gcd(a+d,b+d)=gcd(a+d,(b+d)-(a+d))=gcd(a+d,b-a),它的第二个参数没有变。那么我们把 gcd 的系数扩展一下:$\gcd(a_1,a_2,…,a_k)=\gcd(a_1,a_2-a_1,a_3-a_2,…,a_k-a_k-1)$
区间加后得:$\gcd(a_1+1,a_2+d,…,a_k+d)=\gcd(a_1,a_2-a_1,a_3-a_2,…,a_k-a_k-1)$
其中后 $k-1$ 项是差分数组,如果要区间修改也只需要改差分数组中的两个数,这样我们就可以用线段树来维护单点加区间查询 gcd 了,至于第一个数,可以用树状数组维护区间修改单点查询gcd。
#include<bits/stdc++.h>
using namespace std;
#define dbg(x) cerr<<#x<<':'<<(x)<<' '
#define dbe(x) cerr<<#x<<':'<<(x)<<endl
#define eb emplace_back
using ll=long long;
using vi=vector<int>;
using vl=vector<ll>;
using tp=tuple<int,int>;
struct Bit{
int n=0;
vl c;
Bit(int n):n(n){c.resize(n+1);}
void add(int x,ll d){
while(x<=n)c[x]+=d,x+=x&-x;
}
ll cha(int x){
ll ans=0;
while(x)ans+=c[x],x-=x&-x;
return ans;
}
};
struct Sgt{
struct sgt{
int l,r;
ll gcd;
};
int n;
vector<XDS>tr;
vl a;
sgt Merge(sgt a,sgt b){
return {a.l,b.r,__gcd(llabs(a.gcd),llabs(b.gcd))};
}
void bud(int l,int r,int u){
if(l==r){
tr[u]={l,r,a[l]};
return;
}
int mi=(l+r)/2;
bud(l,mi,u*2);
bud(mi+1,r,u*2+1);
tr[u]=Merge(tr[u*2],tr[u*2+1]);
}
Sgt(int n,vl a):n(n),a(a){
tr.resize(n*4+1);
bud(1,n,1);
}
void add(int l,int u,ll d){
if(tr[u].l==l&&tr[u].r==l){
tr[u].gcd+=d;
return;
}
int mi=(tr[u].l+tr[u].r)/2;
if(l<=mi)add(l,u*2,d);
else add(l,u*2+1,d);
tr[u]=Merge(tr[u*2],tr[u*2+1]);
}
ll cha(int l,int r,int u){
if(l<=tr[u].l&&tr[u].r<=r)return tr[u].gcd;
int mi=(tr[u].l+tr[u].r)/2;
if(r<=mi)return cha(l,r,u*2);
else if(l>mi)return cha(l,r,u*2+1);
else return __gcd(llabs(cha(l,r,u*2)),llabs(cha(l,r,u*2+1)));
}
};
int main(){
cin.tie(0)->sync_with_stdio(0);
int n,m;
cin>>n>>m;
vl a(n+1),cf(n+2);
Bit bit(n+1);
for(int i=1;i<=n;i++){
cin>>a[i];
cf[i]=a[i]-a[i-1];
bit.add(i,cf[i]);
}
cf[n+1]=-a[n];
bit.add(n+1,cf[n+1]);
Sgt sgt(n+1,cf);
char op;
int l,r;
ll d;
while(m--){
cin>>op>>l>>r;
if(op=='C'){
cin>>d;
bit.add(l,d);bit.add(r+1,-d);
sgt.add(l,1,d);sgt.add(r+1,1,-d);
}else if(op=='Q'){
if(l==r)cout<<llabs(bit.cha(l))<<endl;
else cout<<llabs(__gcd(bit.cha(l),sgt.cha(l+1,r,1)))<<endl;
}
}
return 0;
}质数
线性筛
埃氏筛大概是:任意整数 $x$ 的倍数都不是质数,因此从小到大遍历每一个 $x$,如果还未被标记则 $x$ 是质数,然后去标记大于等于 $x^2$ 的 $x$ 的所有倍数。复杂度为 $O(n \log \log n)$。
显然埃氏筛还是会重复标记合数,“根本原因是没有确定出唯一的产生 $x$ 的方法”。线性筛则是保证了只有 $x$ 的最小的质因数才会标记 $x$,详细的算法原理可以去 OI Wiki。代码是这样的:
vi prm,v(N+1);
for(int i=2;i<=N;i++){
if(v[i]==0)v[i]=i,prm.eb(i);
for(auto p:prm){
if(p*i>N||v[i]<p)break;
v[i*p]=p;
}
}建议理解原理后即可背下。
欧拉函数
定义:$\varphi (n)$ 为 $1\sim n$ 中与 $n$ 互质的数个个数。
若 $n=\prod \limits_{i=1}^{m}p_i^{c_i}$ 则 $\varphi (n)=n\times \prod \limits_{i=1}^{m}(1-\frac{1}{p_i})$,使用 $n$ 减去与 $n$ 不互质的数并化简即可推出。
显然计算 $\varphi (n)$ 只需对 $n$ 分解质因数即可:
int phi=n;
for(int i=2;i*i<=n;i++){
if(n%i!=0)continue;
phi=phi/i*(i-1);
while(n%i==0)n/=i;
}
if(n>1)phi=phi/n*(n-1);性质:
- $1\sim n$ 中与 $n$ 互质的数的和为 $\frac{n\times\varphi (n)}{2}$(与 $n$ 互质的数总是成对出现)
- 欧拉函数是积性函数,即若 $a,b$ 互质,则 $\varphi (ab)=\varphi(a)\varphi(b)$。
- $\sum \limits_{d|n} \varphi(d)=n$
线性求欧拉函数
在线性筛的基础上计算欧拉函数:
vi prm,v(N+1),phi(N+1);
phi[1]=1;
for(int i=2;i<=N;i++){
if(v[i]==0)v[i]=i,prm.eb(i),phi[i]=i-1;
for(auto p:prm){
if(p*i>N||v[i]<p)break;
v[i*p]=p;
phi[i*p]=phi[i]*(p-(p<v[i]));//为了防止避免浮点运算所以对原式做些变化
}
}拓展欧几里得
也就是俗称的 exgcd:求 $ax+by=\gcd(a,b)$ 的整数解。
首先我们需要裴蜀定理,定理内容如下:
设 $a,b$ 是不全为零的整数,则:
- 对于任意整数 $x,y$ ,都有 $\gcd(a,b)\mid ax+by$ 成立。
- 存在整数 $x,y$ ,使得 $ax+by=\gcd(a, b)$ 成立。
因为 $a,b$ 都是 $\gcd(a,b)$ 的倍数,所以第一条显然成立。
对于第二条我们可以通过构造的方式证明,也就是 exgcd 求解的过程了:
既然 exgcd 的名字里有 gcd 了,显然与 gcd 有关。我们只考虑 $\gcd(a,b)=1$ 的情况,如果不为 1 只需讲方程两边同时除去 $\gcd(a,b)$ 即可。
回想 gcd 如何通过递归求解:我们可以将原方程变为 $bx’+(a%b)y’=1$,这样一直操作到最后能得到 $ax^{若干’}+by^{若干’}=1$,其中 a=1(即 $\gcd(a,b)$)b=0(gcd 递归的终止条件)。显然有的一组解为 $x^{若干’}=1,y^{若干’}=0$。
那么求出 $bx’+(a%b)y’=1$ 的解与原方程的解的关系就可以求出原方程的解了:
$$\begin{array}{l}
bx’+(a\%b)y’\\
=bx’+(a-b\left\lfloor\frac{a}{b}\right\rfloor)y’\\
=bx’+ay’-b\left\lfloor\frac{a}{b}\right\rfloor y’\\
=ay’+b(x’-\left\lfloor\frac{a}{b}\right\rfloor y’)\\
\therefore ax+by=1的解为\begin{cases}x=y’\\y=x’-\left\lfloor\frac{a}{b}\right\rfloor y’\end{cases}
\end{array}$$
上面这一坨没什么好背的,只要知道 gcd 怎么求就可以在考场上直接推出来。
显然 exgcd 函数也能帮助我们求 $\gcd(a,b)$,所以我们可以将 x,y 作为可被修改的参数传入函数,而函数的返回值是 $\gcd(a,b)$。代码:
function<int(int,int,ll&,ll&)>exgcd=[&](int a,int b,ll& x,ll& y){
if(b==0){x=1,y=0;return a;}
int d=exgcd(b,a%b,y,x);
y-=a/b*x;//为了少写点(毕竟是模板)所以做一些变化
return d;
};exgcd 可用于求同余方程 $ax\equiv \gcd(a,b)\pmod b$ 的解。
推广至多个整数
拓展拓展欧几里得算法(雾),定理如下:
设 $a_1,a_2,\cdots,a_n$ 是不全为零的整数,则:
- 对于任意整数 $x_1,x_2,\cdots,x_n$,都有 $\gcd(a_1,a_2,\cdots,a_n)\mid a_1x_1+a_2x_2+\cdots+a_nx_n$ 成立。
- 存在整数 $x_1,x_2,\cdots,x_n$,使得 $\gcd(a_1,a_2,\cdots,a_n)=a_1x_1+a_2x_2+\cdots+a_nx_n$ 成立。
第一条依旧显然,第二条我们可以用数学归纳法证明:根据 $\gcd(a_1,a_2,\cdots,a_n)=\gcd(\gcd(a_1,a_2,\cdots,a_{n-1}),a_n)$,对 $n$ 进行归纳即可。
裴蜀定理给出了一个整数能够表示为若干个整数的整系数线性组合的充分必要条件,即:
若 $b=a_1x_1+a_2x_2+\cdots+a_nx_n$,其中 $a_i,b$ 均为整数,则该方程有整数解当且仅当 $\gcd(a_1,a_2,\cdots,a_n)\mid b$,然后利用 exgcd 对其进行求解即可。
逆元
定义:$a^{-1}$ 为 $a$ 的逆元。
有什么用呢?在模运算意义下,+,-,*,^ 都是可以直接算的,但除法就不行。但除以一个数等于乘以它的逆元,因此我们求出一个数的逆元就能将除法转换成乘法了。那么如何求解?
F1:
显然 $a\times a^{-1}\equiv 1\pmod m$,这是什么,这是 exgcd!用 exgcd 就可以求了(前提为 $\gcd(a,m)=1$ 才能求)。
F2:
同余中有一条定理为若 $a,m$ 互质则 $a^{b}\equiv a^{b \mod \varphi(m)}\pmod m$。那么如果 $a,m$ 互质,$a^{-1}\equiv a^{-1 \mod \varphi(m)}\pmod m$,有什么用呢?你可以将 $\varphi(m)$ 求出,不过大多数情况下模数应该是个质数,那么 $\varphi(m)$ 就等于 $m-1$,即 $a^{-1}\equiv a^{m-2}\pmod m$,这又是什么,这是快速幂!
线性求逆元
顾名思义,我们需要通过线性的复杂度求出 $1\sim n$ 中所有数的逆元。求单个逆元的复杂度是 $\log$ 的,但整体求显然我们可以做出一些优化,例如之前线性求欧拉函数就可以通过递推求解。
F1
如果你只需要求 $1\sim n$ 的所有逆元,可以用一下方法推导:
$$\begin{array}{l}
假设我们已经求出 1\sim i-1 的所有逆元\\
现在要求方程 i^{-1}\equiv x\pmod p 的解\\
设 p=k\times i+r(其中0\le r\lt i) 则\\
k\times i+r\equiv p\equiv 0\pmod p\\
k\times i\equiv -r\pmod p\\
-k\equiv r\times i^{-1}\pmod p\\
i^{-1}\equiv -\frac{k}{r}\pmod p\\
这里能直接除r是因为r\le i-1,它的逆元是已知的\\
i^{-1}\equiv -p/i\times (p\%i)^{-1}\\
\therefore i^{-1}=(p-p/i)\times (p\%i)^{-1}\% p
\end{array}$$
我们便可写出一下代码:
vi inv(n+1);
inv[1]=1;
for(int i=2;i<=n;i++){
inv[i]=ll(p-p/i)*inv[p%i]%p;
}F2
不过呢,一般需要 $1\sim n$ 的逆元的话,大概就是组合计数了,那么此时我们还需要 $1!\sim n!$ 的逆元,就需要换种方法递推了。
我们用 fct[i] 表示 $i!$,用 inv[i] 表示 $i$ 的逆元,用 invfct[i] 表示 $i!$ 的逆元,便可得到以下代码:
vi fct(n+1),inv(n+1),invfct(n+1);
fct[0]=1;
for(int i=1;i<=n;i++){//递推求 1!~n! (mod p)
fct[i]=(ll)fct[i-1]*i%p;
}
invfct[n]=ksm(fct[n],p-2);//使用快速幂求逆元(前提题目保证p为质数),快速幂函数就省略不写了
for(int i=n;i>=1;i--){//注意是倒着推
inv[i]=(ll)fct[i-1]*invfct[i]%p;// i^-1=1/i=(i-1)!/i!=fct[i-1]*invfct[i]
invfct[i-1]=(ll)i*invfct[i]%p;// 1/(i-1)!=i/i!=i*invfct[i]
}组合计数中通常情况下不会用到 inv 数组,可适当省略。
数论分块
举个栗子,令 $f(x)$ 为 $x$ 的约数个数,求 $\sum\limits_{i=1}^{n} f(i)$。
如果你直接将每个 $f(i)$ 都求出的话,复杂度是 $O(n\sqrt n)$ 的,智慧的 OIer 们是不能接受的,因此我们要换个角度来想:$1\sim n$ 中有 $i$ 这个因数的数的个数,是 $\left\lfloor\frac{n}{i}\right\rfloor$ 个。
$\sum\limits_{i=1}^{n} \left\lfloor\frac{n}{i}\right\rfloor$ 直接求就是 $O(n)$ 的,不过这是经典的数论分块。你可以随便取一个 $n$,最好是质数,然后列出所有的 $\left\lfloor\frac{n}{i}\right\rfloor$,你会发现每种 $\left\lfloor\frac{n}{i}\right\rfloor$ 是连续出现的(区间),且一共有 $\sqrt n$ 种。那么现在我们知道一个区间的左端点 $l$,它的右端点就是 $\left\lfloor\frac{n}{\left\lfloor\frac{n}{i}\right\rfloor}\right\rfloor$,套娃(
int sum=0;
for(int l=1,r;l<=n;l=r+1){
r=n/(n/l);
sum+=(r-l+1)*(n/l);
}那么现在,我们成功将 $O(n\sqrt n)$ 优化成了 $O(\sqrt n)$,为什么会减少这么多?首先看最暴力的 $O(n\sqrt n)$ 的做法,在求每个 $f(i)$ 时,我们需要扫描所有小于等于 $\sqrt i$ 的数然后去统计约数个数,但这 $\sqrt i$ 个数中并不是所有的数都对答案有贡献,所以这个方法浪费了很多时间。将其转化成 $\sum\limits_{i=1}^{n} \left\lfloor\frac{n}{i}\right\rfloor$ 后,通过列表我们又发现不同的 $i$ 求出的 $\frac{n}{i}$ 是有重复的数的,且是有规律的。顺着规律化简就又去掉了许多重复的计算,最终得到了 $O(\sqrt n)$ 的复杂度。
这就是数学题常见的优化思想。
组合计数
省流:哦不!
加法原理,乘法原理,$A_n^m$,$C_n^m=\frac{n!}{m!(n-m)!}$ 这几个基本的定义就不说了,不过 $C_n^m$ 通常被写作 $\binom{n}{m}$,主要说的是 $C_n^m$ 的性质:
- $C_n^m=C_n^{n-m}$
- $\sum\limits_{k=0}^{n} C_n^k=2^n$
- $C_n^m=C_{n-1}^m+C_{n-1}^{m-1}$
根据定义它们都是显然的,最后一条被用作递推求 $C_i^j$,但这是 $O(n^2)$ 复杂度的,太慢了。我们应该直接根据它的定义去算,上文已经讲过如何递推求 $1\sim n$ 的阶乘的逆元,这里直接用就可以了。
模数不是质数
在逆元中我们提到了几种常数或线性求逆元的方式,但这些方式都有一个前提:$a$ 与 模数 $m$ 互质时 $a$ 才有逆元。在模 $m$ 意义下如果 $a$ 不与 $m$ 互质,我们就没办法做除法运算。
所以 $m$ 不是质数时我们就没办法求组合计数了吗?还是有办法的。
我们已知 $\binom{n}{m}$ 一定是个整数,毕竟 $n$ 个球里选出 $m$ 个的方案数不可能为小数。因此对于组合数的定义 $\binom{n}{m}=\frac{\prod\limits_{i=n}^{n-m+1}i}{\prod\limits_{i=m}^{1}i}$ 中,$\prod\limits_{i=n}^{n-m+1}i$ 一定是 $\prod\limits_{i=m}^{1}i$ 的倍数。
因此我们可以将分子和分母进行质因数分解,对于每一个质因子,用分子的系数减去分母的系数就是答案中的系数。这样我们就避免了除法运算。
用到此方法的题目:P3200[HNOI2009] 有趣的数列(真有趣)
二项式定理
$(a+b)^n=\sum\limits_{k=0}^{n}\binom{n}{k} a^k b^{n-k}$
将 $(a+b)^n$ 全部展开后,$a^k b^{n-k}$ 的系数就是 $C_n^k$(选 $k$ 个 $a$,剩下的是 $n-k$ 个 $b$),很显然。
Catalan 数
也就是卡特兰数,其最经典的定义是“0 和 1 各有 $n$ 个,将它们排序得到一个长度为 $2n$ 的序列且满足任意前缀中 0 的个数不少于 1 的个数的序列的数量”,而其最经典的用法就是这题:P1044[NOIP 2003 普及组] 栈。
对于卡特兰数的求解,常见的公式有以下几种:
- $C_i=\left\{\begin{matrix}
\sum\limits_{i=1}^{n}C_{i-1}C_{n-i} & n\ge 2,n\in N_+\\
1 & i=0,1
\end{matrix}\right.$ - $C_i=\binom{2i}{i}-\binom{2i}{i-1}=\frac{\binom{2i}{i}}{i+1}=\frac{\prod\limits_{j=i+2}^{2i}j}{\prod\limits_{j=1}^{i}j}$
- $C_i=C_{i-1}\frac{4i-2}{i+1}$
【1的证明过程】
至于 3 应该是可以通过 1 来证的,所以我懒得写了。
多重集(可重集)
多重集 $S=\{n_1\cdot a_1,n_2\cdot a_2,\dots ,n_k\cdot a_k\}$ 表示 $S$ 由 $n_i$ 个 $a_i(1\le i\le k)$ 组成的。令 $n=\sum\limits_{i=1}{k} n_i$,则 $S$ 的全排列(考虑顺序)个数为:
$$
\begin{array}{l}
\binom{n}{n_1}\binom{n-n_1}{n_2}\binom{n-n_1-n_2}{n_3}\dots\binom{n_k}{n_k}\\
=\frac{n!}{n_1!(n-n_1)!}\frac{(n-n1)!}{n2!(n-n_2)!}\dots \frac{n_k!}{n_k!} \\
=\frac{n!}{\prod_{i=1}^{k}n_i}
\end{array}
$$
如何求从 $S$ 中取出 $r(r\le n_i)$ 个数的组合数(不考虑顺序)个数?原问题等价于求 $x_1+x_2+\dots x_k=r$($x_i$ 为自然数)的解的数量,这是我们小奥里面的的插板法。最后可以得到答案为 $\binom{k+r-1}{k-1}$。【对于 $r$ 更一般的情况则需要用到容斥原理】
矩阵乘法
矩阵可以理解为一个二维数组,如果我们现在有一个 $n$ 行 $m$ 列的矩阵 $a$ 和一个 $m$ 行 $p$ 列的矩阵 $b$,它们相乘得到一个 $n$ 行 $p$ 列的矩阵 $c$(即 $a\cdot b=c$),则
$$c_{i,j}=\sum\limits_{1\le k\le m}{a_{i,k}b_{k,j}}$$
当然这只是一种常用的定义,在不同题目中可以有不同的定义,但称它们为“乘法”是因为它们具有结合律,与乘法类似可以使用快速幂。
那么对于一个矩阵,你只需要重定义*运算符就可以用原来的快速幂模板来做矩阵快速幂了。
矩阵有什么用处呢,例如求斐波那契数列第 $n$ 项。
斐波那契数列的定义为:
$$fb_i=\left\{\begin{matrix}1 & i=0,1\\fb_{i-1}+fb_{i-2} & other\end{matrix}\right.$$
现在我们有一个矩阵 $\begin{bmatrix}fb_i & fb_{i+1}\end{bmatrix}$,如果我们将它与 $\begin{bmatrix}0 & 1\\1 & 1\end{bmatrix}$ 做矩阵乘法,你会发现你可以得到 $\begin{bmatrix}fb_{i+1} & fb_{i+2}\end{bmatrix}$。因此我们可以使用矩阵快速幂进行求解。
重定义乘法运算符:
struct JZ{
vector<vl>a;
int n,m;
JZ(){}
JZ(vector<vl>&a):a(a),n(a.size()){
m=(a.size()?a[0].size():0);
}
JZ(int n,int m):n(n),m(m){
a.resize(n,vl(m));
}
friend JZ operator*(const JZ& a,const JZ& b){
vector<vl>c(a.n,vl(b.m));
for(int i=0;i<a.n;i++){
for(int j=0;j<b.m;j++){
for(int k=0;k<a.m;k++){
c[i][j]+=a.a[i][k]*b.a[k][j];//这里要根据题目而改变
}
}
}
return c;
}
};高斯消元
高斯消元这个算法干的事就是“给定 $n$ 个 $m$ 元一次方程构成的线性方程组,用 $O(n^2m)$ 的复杂度对其求解”,其中线性方程组是指形如下式的方程组:
$$ \begin{cases} a_{1, 1} x_1 + a_{1, 2} x_2 + \cdots + a_{1, m} x_m = b_1 \\ a_{2, 1} x_1 + a_{2, 2} x_2 + \cdots + a_{2, m} x_m = b_2 \\ \vdots \\ a_{n,1} x_1 + a_{n, 2} x_2 + \cdots + a_{n, m} x_m = b_n \end{cases}$$
我们在幼儿园小班就学过如何在数学中解这个方程组,而高斯消元就是直接模拟这个过程。
首先我们可以将一个线性方程组化简为一个矩阵便于编写程序:将每个方程中元的系数和等号右侧的常数提取出来放入 $n*(m+1)$ 的矩阵中,这个矩阵被称为“增广矩阵”。也就是上面写的方程组可以被转化为下面的矩阵:
$$\begin{bmatrix}
a_{1,1} & a_{1,2} & \dots & a_{1,m} & b_1\\
a_{2,1} & a_{2,2} & \dots & a_{2,m} & b_2\\
\vdots & \vdots & & \vdots & \vdots\\
a_{n,1} & a_{n,2} & \dots & a_{n,m} & b_n
\end{bmatrix}$$
而求解这个方程的的步骤可以看做是以下 3 种操作(称为“初等行变换”,同理我们也可以定义矩阵的”初等列变换“):
- 交换第 $i$ 行和第 $j$ 行
- 将第 $i$ 行乘 $x$ 后加到第 $j$ 行
- 将第 $i$ 行乘 $x$
我们在写代码时可以将矩阵的每一行作为一个结构体来写,那么对于操作 1 我们可以通过 swap 两个结构体实现,对于操作 2 我们只需要重定义结构体的加法和乘法的运算符即可,而操作 3 则是用于最终求解答案的,且被包含在操作 2 中了。
我们定义一个变量 $j$ 表示当前处理到第几个元,初值为 1,现在我们可以依次对第 $i$ 行进行如下步骤:
- 在第 $i$ 到 $n$ 行找到“第 $j$ 列不为 0”的行,将这一行与第 $i$ 行交换,即进行“初等行变换”中的操作 1。如果找不到则 $j++$,然后重复此步骤直到找到或 $j>m$。
- 通过“初等行变换”中的操作 2 将除了第 $i$ 行以外的所有行的第 $j$ 列变为 0。
最终我们会得到一个形如以下矩阵的矩阵,其中 0 表示一定为 0 的数,1 表示一定不为 0 的数,2 表示任意实数:
1222222222
0122222222
0000122222
0000012222
0000001222
0000000001
0000000000这个矩阵被称为“对角矩阵”,顾名思义。对于第 $j(1\le j\le m)$ 个元,如果第 $j$ 列中只包含 0 和 2 ,则这个元是一个“自由元”,否则是一个“主元”。根据幼儿园小班的芝士可知:线性方程组方程组无解当且仅当存在一个方程使得 $m$ 个元的系数全部为 0 但等号右侧的常数不为 0。而当方程有解时显然满足:所有自由元的取值任意,也就是如果一个有解的方程组中存在自由元则该方程组有无穷解,反之如果没有自由元则该方程组有唯一解。当所有自由元的取值确定后,所有主元的取值就唯一确定。
综上我们就可以写出以下代码(P3389 【模板】高斯消元法):
#include<bits/stdc++.h>
using namespace std;
#define dbg(x) cerr<<#x<<':'<<(x)<<' '
#define dbe(x) cerr<<#x<<':'<<(x)<<endl
#define eb emplace_back
using ll=long long;
using vi=vector<int>;
using vl=vector<ll>;
using tp=tuple<int,int>;
using db=long double;
db eps=1e-7;
bool is0(db x){return -eps<x&&x<eps;}//db一定要记得精度问题!
struct FC{//FC,顾名思义,方程
int m;//方程中元的个数
vector<db>a;//方程等号左侧每个元的系数
db b;//方程等号右侧的常数
FC(){}
FC(int m):m(m){a.resize(m+1);}
friend ostream& operator<<(ostream& os,const FC& x){
for(int i=1;i<=x.m;i++)os<<x.a[i]<<" ";
os<<"| "<<x.b;
return os;
}
friend istream& operator>>(istream& is,FC& x){
for(int i=1;i<=x.m;i++)is>>x.a[i];
is>>x.b;
return is;
}//为方便输入输出和调试,我们重定义结构体的输入输出
friend FC operator*(FC x,db y){
for(int i=1;i<=x.m;i++)x.a[i]*=y;
x.b*=y;
return x;
}
friend FC operator+(FC x,FC y){
for(int i=1;i<=x.m;i++)x.a[i]+=y.a[i];
x.b+=y.b;
return x;
}
};
int main(){
cin.tie(0)->sync_with_stdio(0);
int n,m;
cin>>n;
m=n;
vector<FC>fc(n+1,FC(m));
for(int i=1;i<=n;i++){
cin>>fc[i];
}
vi zy(m+1);//若zy[i]=0则表示自由元,否则表示约数该主元的方程是第几个
for(int i=1,j=1;i<=n&&j<=m;i++,j++){//按照文章模拟即可
while(j<=m){
bool sf=false;
for(int k=i;k<=n;k++){
if(!is0(fc[k].a[j])){
swap(fc[i],fc[k]);
sf=true;
break;
}
}
if(!sf)j++;
else break;
}
if(j>m)break;
zy[j]=i;
for(int k=1;k<=n;k++){
if(is0(fc[k].a[j])||k==i)continue;
db o=-fc[k].a[j]/fc[i].a[j];
fc[k]=fc[k]+fc[i]*o;
}
}
bool no_sol=false,inf_sol=(*min_element(zy.begin()+1,zy.end())==0);
//分别表示无解和有无穷解
for(int i=1;i<=n;i++){//依次看每个方程是否无解
if(is0(fc[i].b))continue;
bool sf=true;//方程中是否所有的系数都为0
for(int j=1;j<=m;j++){
if(!is0(fc[i].a[j])){sf=false;break;}
}
if(sf){no_sol=true;break;}
}
if(no_sol||inf_sol)cout<<"No Solution\n";
else{
cout<<fixed<<setprecision(2);
for(int j=1;j<=m;j++){
cout<<fc[zy[j]].b/fc[zy[j]].a[j]<<endl;
}
}
// for(int i=1;i<=n;i++)dbg(i),dbe(fc[i]);
return 0;
}代码风格真是越来越像AI了打比赛应该不会被洛谷判作弊吧
0/1分数规划
给定两个长度为 $n$ 的数组 $a,b$,求一组解 $x_i(1\le i\le n)$ 使下式最大化:
$$\frac{\sum\limits_{i=1}^{n}a_ix_i}{\sum\limits_{i=1}^{n}b_ix_i}$$
我们使用惊人注意力二分一个 $L$,其 check 函数为是否存在一组解满足 $\sum\limits_{i=1}^{n}(a_i-Lb_i)x_i\ge 0$,容易发现 check 具有单调性。
那么如何判定是否存在一组解满足 $\sum\limits_{i=1}^{n}(a_i-Lb_i)x_i\ge 0$ 呢?显然所有的 $(a_i-Lb_i)$ 中只要有一个非负数,该不等式就有解。这样我们就得到了一个 $O(n\log n)$ 复杂度的 0/1 分数规划算法。
min/max
首先 $\min$ 和 $\max$ 最基本的转换是 $\min(x,y)=x+y-\max(x,y),\max(x,y)=x+y-\min(x,y)$。
它们各自单独的转换是 $\min(x,y)=\frac{x+y-|x-y|}{2},\max(x,y)=\frac{x+y+|x-y|}{2}$。
转换:像 $\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\min(|a_i-a_j|,|b_i-b_j|)$ 这样的式子,显然 $\min$ 无法直接拆开,尝试递推等思想后依旧无法解决,那么我们只能看看 $\min$ 本身如何转换了。
如果直接转换得到 $\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\frac{|a_i-a_j|+|b_i-b_j|-||a_i-a_j|-|b_i-b_j||}{2}$,还是【待填坑】
切比雪夫距离
定义:$(x1,y1)$ 与 $(x2,y2)$ 的切比雪夫距离为 $\max(|x1-x2|,|y1-y2|)$,即 $(x1,y1)$ 走到 $(x2,y2)$($(x1,y1)$ 在 $(x2,y2)$ 的左下方),每步只能向上,向右,向右上走,最少几步能走到。
【待填坑】
算法杂项
高维前缀和/差分
高维前缀和
这是普通的一维前缀和:
vi qz(n+1);
for(int i=1;i<=n;i++)qz[i]+=qz[i-1];
auto sum=[&](int l,int r){
return qz[r]=qz[l-1];
};这是普通的二维前缀和:
vector<vi>qz(n+1,vi(m+1));
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
qz[i][j]+=qz[i-1][j]+qz[i][j-1]-qz[i-1][j-1];
}
}
auto sum=[&](int x1,int y1,int x2,int y2){
return qz[x2][y2]-qz[x2][y1-1]-qz[x1-1][y2]+qz[x1-1][y1-1];
};一维和二维都可以凭借想想直接推导出公式,但是当维度达到更高的时候就不好想象了,所以我们需要 $n$ 维前缀和的通解。
首先我们先写出 $n$ 维前缀和的定义:
$S_{i_1,\dots,i_n}=\sum\limits_{i’_1\le i_1}\dots\sum\limits{i’_n\le i_n}A{i’_1,\dots,i’_n}$
使用惊人注意力不难发现,$n$ 维前缀和就是 $n$ 次求和。所以我们可以每次只考虑一个维度,固定其余维度,然后求若干个一维前缀和,这样对于每个维度分别求和后就可以得到 $n$ 维前缀和。
vector<vi>qz(n+1,vi(m+1));
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
qz[i][j]+=qz[i-1][j];
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
qz[i][j]+=qz[i][j-1];
}
}vector<vector<vi>>qz(n+1,vector<vi>(m+1,vi(p+1)));
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
for(int k=1;k<=p;k++){
qz[i][j][k]+=qz[i-1][j][k];
}
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
for(int k=1;k<=p;k++){
qz[i][j][k]+=qz[i][j-1][k];
}
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
for(int k=1;k<=p;k++){
qz[i][j][k]+=qz[i][j][k-1];
}
}
}这样就可以求出高维前缀和,至于查询高维区间和我就不知道了。
特殊高维前缀和(枚举子集)
例题:有 $n(1\le n\le 21)$ 个物品和 $m(1\le m\le 10^4)$ 个条件,第 $i$ 个条件为集合 $T_i$ 和权值 $x_i$。定义物品集合 $S$ 的权值为:$S=\sum\limits_{i=1}^{m}x_i\times[T_i\in S]$。现在要求出所有可能的 $S$ 的权值。
首先 $n$ 只有 21,不难想到用二进制进行状态压缩。然后枚举维度计算前缀和即可:
vi qz(1<<n);
for(int k=0;k<n;++k){
for(int i=0;i<n2;++i){
if((i>>k)&1){
qz[i]+=qz[i^(1<<k)];
}
}
}高维差分
【突然发现我好像不会啊】
杂项
除了算法杂项以外的杂项。
语法
三目运算
语法为 条件?如果为真返回值:如果为假返回值,拿 gcd 举例 return b?gcd(b,a%b):a 和 if(b==0)return a;else return gcd(b,a%b); 是一样的效果,更加的简短豪康了。
至于运算优先级的问题,保险起见你最多在整条语句外面加个括号,是为了防止语句内的其他运算跟外面的运算出问题,?: 这个运算本身不会出什么问题,它不可能再被解释成其他的语句了。
Lambda表达式
简单地说,就是能把一切东西都往 main 函数里塞的工具。
常用的形式大概是这样的:
auto f=[&](int a,int b){
//↑auto 能自动根据你的返回值推断出表达式的类型,这里实际的类型为function<string(int,int)>
// ↑ &表示函数中可以读取和修改外部变量,不写&则表示不能使用或修改外部变量
// ↑跟普通函数一样,这里是调用f时需传的参数
//函数内容
return str;//返回值为string
};//注意这只是个表达式,一条语句,f从某种角度来说还是个被定义的变量,这里需要分号!但是当你想让函数自己调用自己的时候就会发现 auto 不智能了,这里有两种办法:一种是手动写上 f 的类型,拿最简单的计算 $\sum\limits_{i=1}^{n}$ 举例:
function<long long/*函数返回值类型*/(int/*所有传进来的参数的类型*/)>f=[&](int n){
if(n==1)return 1ll;//lambda表达式中所有的返回值类型必须相同,也就是这里不可以返回(int)1
return f(n-1)+n;
};//分号!第二种是把函数塞到参数里,这种方法的好处是常数小,坏处是不管在哪调用函数都要多写一个参数。我们用并查集举个栗子:
auto fa=[&](int x,auto&&self){
return f[x]=(f[x]==x?x:self(f[x],self);
};
//调用:
int U=fa(u,fa);cout保留精度
因为在使用了 cin.tie(0)->sync_with_stdio(0); 后便无法使用 printf("%.2f",x); 去保留精度。因此我们需要使用 cout<<fixed<<setprecision(2)<<x; 来达到同样的效果。
随机数
使用 mt19937 rnd(seed); 创建一个随机数函数。
使用 shuffle(a.begin(),a.end(),rnd) 随机打乱指定序列。
一些函数
为了体现出迭代器的伟大,让我们在这里放一些用于简化代码的函数。
fill
fill(v.begin(),v.end(),x);将v.begin()到v.end()指向的元素赋值为任意数值 x,复杂度线性,也是按位赋值所以常数同 memset 一样小,但也只能赋值整数等,不能赋值结构体之类的东西。
reverse
reverse(v.begin(),v.end());翻转v中的元素,复杂度线性。(这玩意儿甚至在 23 年 J 组初赛时考到了)
memcpy
memcpy(a,b,sizeof b); 按位将 $b$ 数组赋值到 $a$ 数组($a,b$ 数组长度相同)。
next_permutation
next_permutation(v.begin(),v.end());将 $v$ 变为 $v$ 的下一个排序,通常配合 do{...}while; 来枚举 $1\sim n$ 的全排列。
iota
iota(v.begin(),v.end()); 将 *(v.begin()+i) 赋值成 i,可用于初始化并查集等。
shuffle
shuffle(v.begin(),v.end(),rnd); 将范围中元素使用传入的随机打乱,用于乱搞和充分发扬人类智慧。
卡常&啸技巧
与算法无关。
max&min
C++11 有个新语法,就是 max 可以用来比较多个数的值:
max({a[1],a[2],a[3]...a[n]});inline
建议编译器对函数进行内联优化。很古老的东西,但是听说是现在的编译器一般都不会采取建议(((在定义的函数前面加上这个东西也许可以加快速度。
stable_sort
归并排序函数,存在的原因是 sort 不稳定而归并排序稳定。
clock
帮助乱搞做法充分发扬人类智慧。
int st=clock();
while(clock()-st<=CLOCKS_PER_SEC*0.8){
...
}需要注意的是,clock() 函数也会浪费一点时间的。
关于多维数组
如果我们现在需要一个大小为 2e5 * 64 的二维整形数组 $a$,为了程序更高的效率,利用计算机缓存,我们应将它写作 int a[64][200005]; 而不是 int a[200005][64];(也就是尽量将范围小的维度开在前面)。这两种写法在数据范围大的情况下可能能有一倍的差距。vector 也同理。
位运算
(这么重要的东西为什么被放在最后呢?就跟 vector<bool> 一样这是上古遗留物)
位运算的特点就是在二进制表示下不会进位,每一位与其他位计算出的值都无关。一些题目下我们便可将数据的值(32 位或 64 位整型)的每一位分别处理。
(2025.10.6 烤咕:最初这篇文章可是用来总结 trick 的啊!)
bitset
bitset 也算是一种数据结构,他能被当做二进制数使用,两个 bitset 之间可以正常的进行按位异或、与、或运算。但是他不止能够存 64 位,类似 bool 数组,你可以将它的大小开到 1e6 都行。两个 bitset 做位运算的时间复杂度为 $O(bitset大小/计算机位数)$,通常来讲计算机位数是 $64$ 位的。
bitset 也常被用作路径压缩(如 dp 时)或集合计算。
当我们想求图上两节点的公共祖先之类的问题时,在 $n^2\le 6\times 10^9$ 的情况下可以考虑使用 bitset 记录每个点是不是一个点的祖先。求祖先交集,将两个节点的 bitset 进行与(&)运算即可。同理,将两个 bitset 进行或(|)运算即可得到并集。
__builtin_
__builtin_clz(x)用于求 $x$ 的二进制数中最高位的1前面有多少个0,常见的用法是用于求 log2(x)=31-__builtin_clz(x)($x$ 为int)或log2(x)=63-__builtin_clzll(x)($x$ 为 longlong)。
__builtin_ctz(x)用于求 $x$ 的二进制数中最低位的1后面有多少个0,__builtin_popcount(x)用于求 $x$ 二进制数中1的个数,需要注意这个函数的参可以传 long long 但是最大只会返回 32(也就相当于求二进制下前 32 位中有多少个 1,不如自己手写一个)。
如何分辨 clz 和 ctz?
clz=Count Leading Zeros
ctz=Count Trailing Zeros
哦对了 clz 还是陈亮舟的缩写
以上函数都是汇编函数,因此基本上就是 $O(1)$ 的,比手写的快,可以放心食用。
OUR TEAM, HAVING A 32,768 THREADS AND A 32th GEN INTEL CORE i16-21,247,483,647H CPU WITH
9,223,372,036,854,775,808GB OF MEMORY TO BLOW YOUR SERVER UP!!!! IF YOU DON’T WRITE BACK AN EMAIL PROMISING U.S.1,145,141,919,810$, BEFORE 12:AM (UTC-4), JUNE 7, 2025, WE WILL IMMEDIATELY DDOS YOU WITH OUR CLIENT VIA 16 VPNS.