第一类斯特林数

定义：将 $n$ 个不同元素划分进 $m$ 个相同的环（不可为空）的方案数，记为 $S_1(n,m)$ 或 ${n\brack m}$（{n\brack m}）。其中“环”指“旋转后重合算同一种方案”的“有序数组”。

递推式：

可以理解为，将 $n$ 加入已经排好的 $n-1$ 个数中：

• $n$ 可以单独划入一个新的环，对应 ${n-1\brack m-1}$ 种方案。
• $n$ 还可以插入到原有的 $m$ 个环中，对应 ${n-1\brack m}\cdot (n-1)$。

相加得到答案。

递推的出口为 ${n\brack 0}=[n=0]$。

第二类斯特林数

定义：将 $n$ 个不同元素划分进 $m$ 个相同的无序集合（不可为空）的方案数，记为 $ S_2(n,m)$ 或 ${n \brace m}$（{n\brace m}）。

递推式：

与第一类斯特林数类似，将 $n$ 加入前 $n-1$ 个数中：

• $n$ 可以单独划入一个新的无序集合，对应 ${n-1\brace m-1}$。
• $n$ 还可以插入到原有的 $m$ 个无需集合中，对应 ${n-1\brace m}m$。

相加得到答案。

递推出口为 ${n\brace 0}=[n=0]$。

通项：

可以通过容斥原理证明：

首先考虑 $m$ 个无需集合互相区分的方案数，记为 $f(n,m)={n\brace m}m!$，即 ${n\brace m}=\frac{f(n,m)}{m!}$

定义全集 $U$ 为：将 $n$ 个不同的元素划分进 $m$ 个不同的无序集合，且集合可以为空的方案。显然每个元素都可以放入 $m$ 个集合中的任意一个，因此 $|U|=m^n$。

定义集合 $P_i$ 为：将 $n$ 个不同的元素划分进 $m$ 个不同的无序集合，集合可以为空，且集合 $i$ 为空的方案。

则根据容斥原理可得：

其中“任意 $k$ 个 $P_i$ 的交集”的小就是“至少有 $k$ 个集合为空的方案数”，方案数为 $\binom{m}{k}(m-k)^n$，即从 $m$ 个集合中选出 $k$ 个集合为空，然后将 $n$ 个元素放入剩下的 $m-k$ 个集合中的方案数。

整理式子可得上述的地推式。

显然直接算的复杂度为 $O(m\log n)$。

例题

例题1（P4609）

题目大意：$T(1\le T\le 2\times 10^5$ 组数据，每组数据给定三个整数 $n,A,B(1\le n\le 5\times 10^4,1\le A,B\le 100$，求有多少种 $1\sim n$ 的排列 $p$ 满足：前缀最大值有 $A$ 个，后缀最大值有 $B$ 个。

首先注意到，排列 $p$ 中的 $n$ 一定是下标最大的前缀最大值，也一定是下标最小的后缀最大值。$p_1$ 一定是前缀最大值， $p_n$ 一定前缀最小值。因此整个排列一定形如下图：

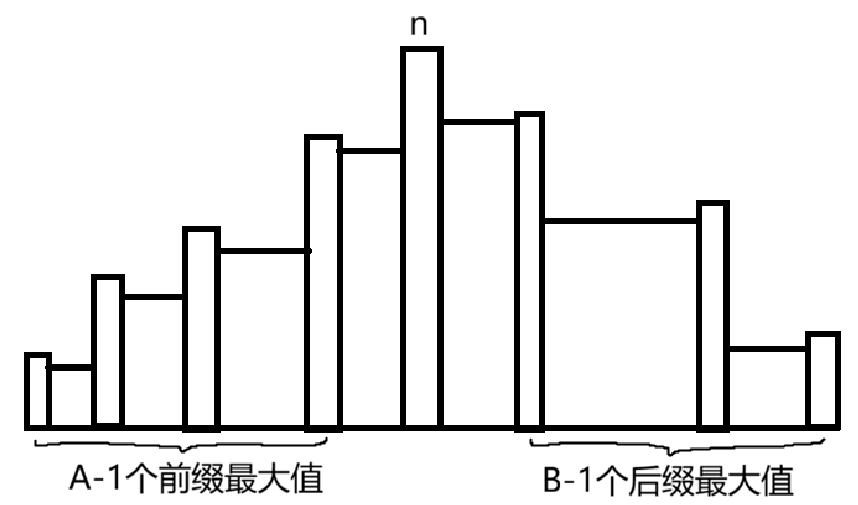
一个前缀最大值到它的下一个前缀最大值之间的数，一定小于这个前缀最大值。后缀最大值同理。因此我们将整个排列看做 $A+B-2$ 个环，每个环中的最大值作为一个前（后）缀最大值。从 $A+B-2$ 个环中选出 $A-1$ 个放在 $n$ 左边，剩下 $B-1$ 个放在 $n$ 右边。每个环内的最大值为关键字进行排序，即可确定唯一的顺序。因此最终答案为：

例题2

有以下三个问题：

1. 给定正整数 $n,m(1\le n,m\le 10^5)$，求将 $n$ 个互相区分的球放入 $m$ 个互不区分的盒子中，且盒子不可以为空的方案数。
2. 给定正整数 $n,m(1\le n,m\le 5000)$，求将 $n$ 个互相区分的球放入 $m$ 个互不区分的盒子中，且盒子可以为空的方案数。
3. 给定正整数 $n,m(1\le n,m\le 10^5)$，求将 $n$ 个互相区分的球放入 $m$ 个互相区分的盒子中，且盒子不可以为空的方案数。

问题 1 就是第二类斯特林数，即 ${n\brace m}$。

问题 2 比问题 1 多了个盒子可以为空的条件，枚举有几个盒子为空，剩下的盒子就不为空，还是第二类斯特林数。最终答案 $\sum\limits_{k=0}^{m}{n\brace m-k}$。

问题 3 就是把问题 1 中的盒子区分一下，把问题 1 的答案乘上 $m!$ 即可。